题目内容
 如图,一次函数y=
如图,一次函数y=| 3 |
| 4 |
| 24 |
| x |
(1)求m,n的值;
(2)求△ADC的面积.
考点:反比例函数与一次函数的交点问题
专题:压轴题
分析:(1)把C点坐标代入反比例函数解析式求出n,得C点坐标,再代入一次函数解析式求m;
(2)根据三角形面积公式即可求解.
(2)根据三角形面积公式即可求解.
解答:解:(1)∵点C(4,n)在y=
的图象上,
∴n=6,
∴C(4,6),
∵点C(4,6)在y=
x+m的图象上,
∴m=3;
(2)
x+3=0,
解得x=-4,
△ADC的面积为:[4-(-4)]×6÷2=24.
| 24 |
| x |
∴n=6,
∴C(4,6),
∵点C(4,6)在y=
| 3 |
| 4 |
∴m=3;
(2)
| 3 |
| 4 |
解得x=-4,
△ADC的面积为:[4-(-4)]×6÷2=24.
点评:本题考查了反比例函数与一次函数图象的交点问题,待定系数法求函数解析式,此类题目的求解一般都是先把已知点的坐标代入反比例函数表达式求出反比例函数解析式,然后再求一次函数解析式,难度中等.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
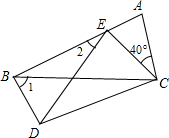 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、120° |
 如图,△ABC中,点D在边AB上,且满足∠ACD=∠ABC,若AC=2,AD=1,则DB的长为( )
如图,△ABC中,点D在边AB上,且满足∠ACD=∠ABC,若AC=2,AD=1,则DB的长为( )| A、1 | B、2 | C、3 | D、4 |
反比例函数y=
的图象经过下列哪个点( )
| 2 |
| x |
| A、(-1,2) |
| B、(-2,1) |
| C、(-1,-2) |
| D、(0,0) |
 如图,已知点A(1,y1)、B(2,y2)是反比例函数y=
如图,已知点A(1,y1)、B(2,y2)是反比例函数y= 如图,双曲线y=
如图,双曲线y=