��Ŀ����
10����ͼ1��ABCD��һ�ž���ֽƬ��AD=BC=1��AB=CD=5���ھ���ABCD�ı�AB��ȡһ��M����CD��ȡһ��N����ֽƬ��MN�۵���ʹMB��DN���ڵ�K���õ���MNK��KB��MN��O����1��������1=80�㣬���MKN=20�㣻
�ڲ�ͬ���۵��õ���ͬ�ġ�MNK����MNK����������ֵΪ$\frac{13}{10}$��
��2����ֽƬ����ͼ2��ʾ�ķ�������KP�۵���ʹ��M���߶�KD�ϣ������۵�������ԭ���ε��غϲ���Ϊ�ı���KPMN�����ı���KPMN�����ΪS��
���ж��ı���KPMN����״����˵�����ɣ�
�����S����Сֵ�����ֵ��
���ı���KPMN�ܳ�Ϊij�������ı�����ָ����ʱ�ۺ�MN��Ҫ����������������S��ֵ��

���� ��1����ֻҪ֤����KNM=��KMN=80�㣬���ɽ�����⣮
����ͼ1�У�����B���D�غ�ʱ����MKN����������DM=x�����ݹ��ɶ����г����̼��ɽ�����⣮
��2���ٽ��ۣ��ı���KPMN��ƽ���ı��Σ�ֻҪ֤��KN=PM��KN��PM���ɣ�
�ڵ���D��M�غϣ���B���K�غ�ʱ��S�����BD=B��D=BD��=x��A��P=C��N=y��������$\left\{\begin{array}{l}{2x+Y=5}\\{{x}^{2}=1+{y}^{2}}\end{array}\right.$���ⷽ���鼴�ɣ���MK��A��B��ʱ�����ݴ��߶���̿�֪��MK����СֵΪ1����ʱS����СֵΪ1��
�۵���NMB��=60���120��ʱ���ı���KPMN�����Σ�������εĸߺͱ߳����ɣ�
��� �⣺��1������ͼ2�У�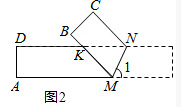
��DN��AM��
���DNM=��1=80�㣬
�ߡ�KMN=��1=80�㣬
���NKM=180��-��KNM-��KMN=20�㣬
�ʴ�Ϊ20�㣮
����ͼ1�У�����B���D�غ�ʱ����MKN����������DM=x��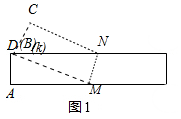
��Rt��AMD��AD=1��AM=5-x��DM=x��
��x2=12+��5-x��2��
��x=$\frac{13}{5}$��
�ɢٿ�֪��DMN=��DNM��
��KN=DM=$\frac{13}{5}$��
���KNM��������ֵΪ$\frac{1}{2}$•$\frac{13}{5}$•1=$\frac{13}{10}$��
�ʴ�Ϊ$\frac{13}{10}$��
��2���ٽ��ۣ��ı���KPMN��ƽ���ı��Σ�
���ɣ���ͼ3�У�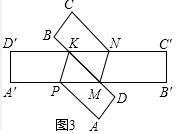
��A��B���C��D�䣬
���KNM=��NMB��=��NMK��
��KN=KM��ͬ����֤KM=PM��
��KN=PM����KN��PM��
���ı���KPMN��ƽ���ı��Σ�
����ͼ4�У�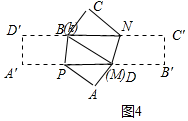
����D��M�غϣ���B���K�غ�ʱ��S�����BD=B��D=BD��=x��A��P=C��N=y��
������$\left\{\begin{array}{l}{2x+Y=5}\\{{x}^{2}=1+{y}^{2}}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{10-\sqrt{22}}{3}}\\{y=\frac{2\sqrt{22}-5}{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{10+\sqrt{22}}{3}}\\{y=\frac{-5-2\sqrt{22}}{3}}\end{array}\right.$����������
��NK=$\frac{10-\sqrt{22}}{3}$��
��S�����ֵ=$\frac{10-\sqrt{22}}{3}$��
��MK��A��B��ʱ�����ݴ��߶���̿�֪��MK����СֵΪ1����ʱS����СֵΪ1��
���ı���KPMN�ܳ�Ϊij�������ı��Σ�����NMB��=60���120��ʱ���ı���KPMN�����Σ�
��ʱ���εĸ�Ϊ1���߳�Ϊ$\frac{2\sqrt{3}}{3}$������S=$\frac{2\sqrt{3}}{3}$��
���� ���⿼���ı����ۺ��⡢ƽ���ı��ε����ʡ����ɶ�������Ԫ���η����顢���ε��ж������ʵ�֪ʶ����һ�������еĢڽ���Ĺؼ�����ȷѰ�ҵ�B��λ�ã��ڶ��������еĢڵĽ���ؼ���ѧ�����÷����������⣬�����п�ѹ���⣮

| A�� | -10�� | B�� | -6�� | C�� | 6�� | D�� | 10�� |
| A�� | a=2��b=3 | B�� | a=-2��b=-3 | C�� | a=2��-2��b=3 | D�� | a=0��b=3 |
| A�� | -2 | B�� | 0 | C�� | $\sqrt{2}$ | D�� | 3 |
| A�� | 0.06=6��10-3 | B�� | -0.000026=-2.6��10-7 | ||
| C�� | 168000=1.68��106 | D�� | 28000000=2.8��107 |
| A�� | -3��$-\frac{1}{3}$ | B�� | |-3|��3 | C�� | $|{-\frac{1}{3}}|$��$-\frac{1}{3}$ | D�� | $-\frac{1}{3}$��$-|{-\frac{1}{3}}|$ |
| A�� | -2 | B�� | 0 | C�� | -1 | D�� | 1 |
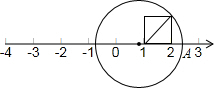 ��ͼ��ʾ��������ĵ�λ�����߶�Ϊ����һ�������Σ��������ϱ�ʾ��1�ĵ�ΪԲ�ģ������ζԽ��߳�Ϊ�뾶�������������������ڵ�A�����A��ʾ�����ǣ�������
��ͼ��ʾ��������ĵ�λ�����߶�Ϊ����һ�������Σ��������ϱ�ʾ��1�ĵ�ΪԲ�ģ������ζԽ��߳�Ϊ�뾶�������������������ڵ�A�����A��ʾ�����ǣ�������| A�� | $\sqrt{2}$ | B�� | $1+\sqrt{2}$ | C�� | 2.4 | D�� | 2.3 |