题目内容

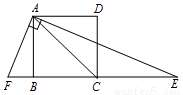
19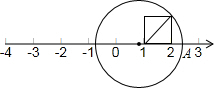．如图所示，以数轴的单位长度线段为边作一个正方形，以数轴上表示数1的点为圆心，正方形对角线长为半径画弧，交数轴正半轴于点A，则点A表示的数是（　　）
A．$\sqrt{2}$B．$1+\sqrt{2}$C．2.4D．2.3

分析 首先求出正方形对角线的长度，再根据点A在数轴上的位置，确定点A表示的数．

解答 解：∵正方形的边长为1，
∴正方形对角线的长度=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，
∴OA=1+$\sqrt{2}$，
故点A表示1+$\sqrt{2}$．
故选：B．

点评 本题考查的是勾股定理，实数与数轴，熟知数轴上各点与实数是一一对应关系是解答此题的关键．

练习册系列答案
相关题目
10．如图1，ABCD是一张矩形纸片，AD=BC=1，AB=CD=5．在矩形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK，KB交MN于O．
（1）①若∠1=80°，求∠MKN=20°；
②不同的折叠得到不同的△MNK，△MNK的面积的最大值为$\frac{13}{10}$．
（2）将纸片按如图2所示的方法再沿KP折叠，使点M在线段KD上，两次折叠部分与原矩形的重合部分为四边形KPMN，设四边形KPMN的面积为S．
①判断四边形KPMN的形状，并说明理由；
②求出S的最小值与最大值；
③四边形KPMN能成为某种特殊四边形吗？指出此时折痕MN需要满足的条件，并求出S的值．
11．已知a+b=5，ab=2，则（a-b）2的值为（　　）
A．21B．25C．17D．13
7．下列结果计算正确的是（　　）
A．（-1）-1=1B．（-1）0=0C．${（-\frac{1}{2}）^{-2}}=-4$D．-（-1）2=-1
14．下列合并同类项正确的是（　　）
A．-2xy-2xy=0B．3a2b-3ab2=0C．3m3+2m3=5m3D．3a2-a2=2
4．如果$\sqrt{2x-1}$有意义，则x可以取的最小整数为（　　）
A．-1B．0C．1D．2

某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.

(1)求该班的学生人数；

(2)若该校初三年级有1 000人,估计该年级选考立定跳远的人数.

据国家统计局网站发布消息，2016年吉林省粮食总产量约为37 172 000吨，将37 172 000用科学记数法表示为（ ）

A. 3.7172×106 B. 3.7172×107 C. 3.7172×108 D. 3.7172×109

如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB延长线于点F，则EF的长为__________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网