题目内容
13.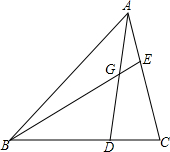 已知△ABC中,BD:DC=3:1,G为AD中点,求EG:GB.
已知△ABC中,BD:DC=3:1,G为AD中点,求EG:GB.
分析 过D作DF∥AC,可得△AEG≌△DFG,即FG=EG,再由平行线的性质可得对应线段成比例,进而即可求解EG:GB的比值.
解答 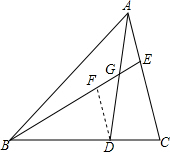 解:过D作DF∥AC交BE于F,
解:过D作DF∥AC交BE于F,
∴∠FDG=∠EAG,
∵G是AD的中点,
∴AG=DG,
在△AEG∽△DFG,$\left\{\begin{array}{l}{∠EAG=∠FDG}\\{AG=DG}\\{∠AGE=∠FGD}\end{array}\right.$,
∴△AEG≌△DFG,
∴FG=EG,
∵DF∥AC,BD:DC=3:1,
∴BF:EF=3:1,
∴EG:BG=1:7.
点评 本题主要考查了全等三角形的判定及性质以及平行线分线段成比例的性质问题,能够熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.$\frac{1}{3}$是3的( )
| A. | 相反数 | B. | 绝对值 | C. | 倒数 | D. | 平方根 |
5.到三角形三个顶点的距离相等的点一定是三角形( )的交点.
| A. | 三条角平分线 | B. | 三条边的垂直平分线 | ||
| C. | 三条高 | D. | 三条中线 |
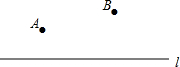 如图,已知直线l及其同侧两点A、B.
如图,已知直线l及其同侧两点A、B.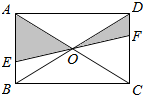 如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为( )
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,若AB=3,BC=4,那么阴影部分的面积为( )