Question

如图，等腰梯形ABCD中，AD∥BC，AD＝3，BC＝7，∠B＝60°，P为BC边上一点（不与B，C重合），过点P作∠APE＝∠B，PE交CD 于E。

(1)求证:△APB∽△PEC；(2)若CE＝3,求BP的长。

Answer 1

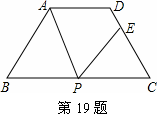
解：(1)证明:梯形ABCD中,∵AD∥BC,AB＝DC

∴∠B＝∠C＝60°       ……………1分

∵∠APC＝∠B＋∠BAP

即∠APE＋∠EPC＝∠B＋∠BAP

∵∠APE＝∠B

∴∠BAP＝∠EPC     ……………1分

∴△APB∽△PEC      ……………1分

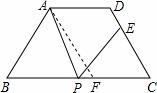
(2)过点A作AF∥CD交BC于F

则四边形ADCF为平行四边形,△ABC为等边三角形    ……………1分

∴CF＝AD＝3,AB＝BF＝7－3＝4

∵△APB∽△PEC,       ……………1分

∴＝

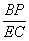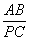
设BP＝x,则PC＝7－x,又EC＝3, AB＝4

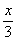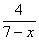∴＝        ……………1分

整理,得x²－7x＋12＝0

解得    x₁＝3,  x₂＝4    ……………1分

经检验, x₁＝3,  x₂＝4是所列方程的根

∴BP的长为3或4           ……………1分