题目内容
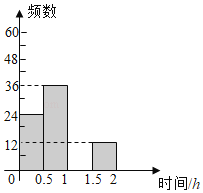
【题目】扬州市“五个一百工程“在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h | 频数 | 频率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合计 | a | 1 |
根据以上信息,回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天课外阅读时间超过1小时的人数.
【答案】(1)120,0.1;(2)见解析;(3)600人
【解析】
(1)由0.5<t≤1的频数与频率可得总人数a,再用12除以总人数可得b的值;
(2)总人数乘以0.4得出第3组频数,从而补全图形;
(3)利用样本估计总体思想可得.
(1)a=36÷0.3=120,b=12÷120=0.1,
故答案为:120,0.1;
(2)1<t≤1.5的人数为:120×0.4=48,
补全图形如下:

(3)估计该校学生每天课外阅读时间超过1小时的人数为:1200×(0.4+0.1)=600(人).

 阅读快车系列答案
阅读快车系列答案【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?
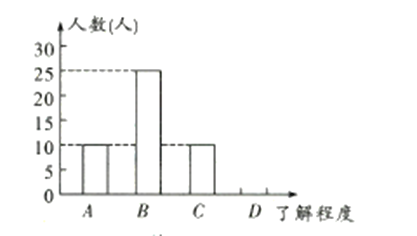
【题目】为响应市政府关于“垃圾不落地,市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的了解情况,对该校部分学生进行了问卷调查,并将调查结果分为![]() 四类(其中
四类(其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
了解程度 | 人数(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生
若该校共有学生![]() 人,估计该校对垃圾分类知识“非常了解”的有多少人?
人,估计该校对垃圾分类知识“非常了解”的有多少人?