题目内容
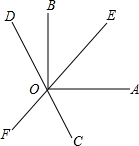 如图,已知直线CD、EF相交于点O,OA⊥OB,且OC平分∠AOF,∠BOE=2∠AOE.求∠BOD的大小.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OC平分∠AOF,∠BOE=2∠AOE.求∠BOD的大小.
解:∵OA⊥OB,
∴∠AOB=90°,
又∵∠BOE=2∠AOE,
∴∠AOE=90°× =30°,
=30°,
∴∠AOF=180°-30°=150°,
又∵OC平分∠AOF,
∴∠AOC=150°× =75°,
=75°,
∴∠BOD=180°-90°-75°=15°.
分析:根据OA⊥OB可知∠AOB=90°,再根据∠BOE=2∠AOE求出∠AOE的度数,再根据OC平分∠AOF和∠AOF+∠AOE=180°,求出∠BOD的大小.
点评:本题考查了角的运算,涉及垂线、角平分线、邻补角等概念,是一道关于角的综合题.
∴∠AOB=90°,
又∵∠BOE=2∠AOE,
∴∠AOE=90°×
 =30°,
=30°,∴∠AOF=180°-30°=150°,
又∵OC平分∠AOF,
∴∠AOC=150°×
 =75°,
=75°,∴∠BOD=180°-90°-75°=15°.
分析:根据OA⊥OB可知∠AOB=90°,再根据∠BOE=2∠AOE求出∠AOE的度数,再根据OC平分∠AOF和∠AOF+∠AOE=180°,求出∠BOD的大小.
点评:本题考查了角的运算,涉及垂线、角平分线、邻补角等概念,是一道关于角的综合题.

练习册系列答案
相关题目
 15、如图,已知直线CD与⊙O相切于点C,AB为直径,若∠BCD=40°,则∠ABC的大小等于
15、如图,已知直线CD与⊙O相切于点C,AB为直径,若∠BCD=40°,则∠ABC的大小等于 如图,已知直线CD、EF相交于点O,OA⊥OB,且OC平分∠AOF,∠BOE=2∠AOE.求∠BOD的大小.
如图,已知直线CD、EF相交于点O,OA⊥OB,且OC平分∠AOF,∠BOE=2∠AOE.求∠BOD的大小. 17、如图,已知直线CD与⊙O相切于点C,AB为直径.若∠BCD=35°,则∠ABC的大小等于
17、如图,已知直线CD与⊙O相切于点C,AB为直径.若∠BCD=35°,则∠ABC的大小等于 如图,已知直线CD经过AB的中点O,OE⊥AB,∠DOE=30°,下列关系:①CO=DO;②OB=
如图,已知直线CD经过AB的中点O,OE⊥AB,∠DOE=30°,下列关系:①CO=DO;②OB=