题目内容
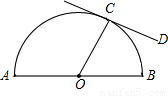
15、如图，已知直线CD与⊙O相切于点C，AB为直径，若∠BCD=40°，则∠ABC的大小等于50
度．分析：根据弦切角定理得∠A=∠BCD=40°，再根据AB是直径，可知∠ACB=90°，进而可求出∠ABC=50°．
解答：
解：连接AC，
根据直线CD与⊙O相切于点C，
则根据弦切角定理得到∠A=∠BCD=40°，
根据AB是直径，
因而∠ACB=90°，
因而∠ABC=50°．
解：连接AC，根据直线CD与⊙O相切于点C，
则根据弦切角定理得到∠A=∠BCD=40°，
根据AB是直径，
因而∠ACB=90°，
因而∠ABC=50°．
点评：本题综合运用了切线的性质定理，直径所对的圆周角是直角，以及弦切角定理．
练习册系列答案
阅读快车系列答案
相关题目
17、如图，已知直线CD与⊙O相切于点C，AB为直径．若∠BCD=35°，则∠ABC的大小等于
