题目内容
等腰△ABC的两边长分别是一元二次方程x2-9x+18=0的两个解，则这个等腰三角形的周长是（ ）
| A、9 | B、12 |
| C、15 | D、12或15 |
考点：解一元二次方程-因式分解法,三角形三边关系,等腰三角形的性质
专题：计算题
分析：先利用因式分解法解方程x2-9x+18=0得x1=3，x2=6，再根据等腰三角形的性质分类：若腰为3，底为6或腰为6，底为3，然后根据三角形三边的关系确定三角形的边长后计算周长．
解答：解：x2-9x+18=0，
（x-3）（x-6）=0，
所以x1=3，x2=6，
当腰为3时，由于3+3=6，不符合三角形三边的关系，故舍去；
当腰为6，底为3，则三角形周长=6+6=3=15．
故选C．
（x-3）（x-6）=0，
所以x1=3，x2=6，
当腰为3时，由于3+3=6，不符合三角形三边的关系，故舍去；
当腰为6，底为3，则三角形周长=6+6=3=15．
故选C．
点评：本题考查了解一元二次方程-因式分解法：因式分解法解一元二次方程的一般步骤：移项，使方程的右边化为零；将方程的左边分解为两个一次因式的乘积；令每个因式分别为零，得到两个一元一次方程；解这两个一元一次方程，它们的解就都是原方程的解．也考查了三角形三边的关系．
练习册系列答案
相关题目
如图所示，写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标，并画出△ABC关于y对称的△A2B2C2．
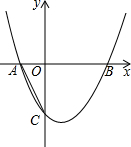如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点，点A在x轴的负半轴，点B在x轴的正半轴，与y轴交于点C，且CO=2AO，CO=BO，AB=3．则下列判断中正确的是（ ）| A、此抛物线的解析式为y=x2+x-2 | ||
| B、当x＞0时，y随着x的增大而增大 | ||
C、此抛物线与直线y=-
| ||
| D、在此抛物线上的某点M，使△MAB的面积等于4，这样的点共有三个 |
已知，在平面直角坐标系中，AB是双曲线y=
有一架5米长的梯子搭在墙上，刚好与墙 头对齐，此时梯脚与墙的距离是3米，若
+（y+2）2=0，则（x+y）2014等于（ ）
| x-1 |
| A、? 1 |
| B、1 |
| C、32014 |
| D、? 32014 |