题目内容
 将矩形纸片ABCD沿折痕EF对折,使点A与C重合.若已知AB=6cm,BC=8cm,求EF的长.
将矩形纸片ABCD沿折痕EF对折,使点A与C重合.若已知AB=6cm,BC=8cm,求EF的长.
分析:连接AE、CF,利用折叠的性质证明四边形AECF为菱形,设AE=EC=x,在Rt△ABC中,由勾股定理求AC,在Rt△ABE中,由勾股定理求x,利用菱形计算面积的两种方法,建立等式求EF.
解答: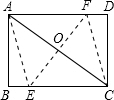 解:连接AE、CF,
解:连接AE、CF,
由折叠可知,EF⊥AC,
又∵AF∥CE,
∴∠FAO=∠ECO,
在△AOF与△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵AC垂直平分EF,
∴AE=AF,
∴四边形AECF为菱形(有一组邻边相等的平行四边形是菱形)
设AE=EC=xcm,则BE=(8-x)cm,
在Rt△ABC中,由勾股定理得:AC=
=10cm,
在Rt△ABE中,由勾股定理得:AB2+BE2=AE2,
即62+(8-x)2=x2,解得x=
,
根据菱形计算面积的公式,得
EC×BA=
×EF×AC,
即
×6=
×EF×10,
解得EF=
cm.
 解:连接AE、CF,
解:连接AE、CF,由折叠可知,EF⊥AC,
又∵AF∥CE,
∴∠FAO=∠ECO,
在△AOF与△COE中,
|
∴△AOF≌△COE(AAS),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵AC垂直平分EF,
∴AE=AF,
∴四边形AECF为菱形(有一组邻边相等的平行四边形是菱形)
设AE=EC=xcm,则BE=(8-x)cm,
在Rt△ABC中,由勾股定理得:AC=
| AB2+BC2 |
在Rt△ABE中,由勾股定理得:AB2+BE2=AE2,
即62+(8-x)2=x2,解得x=
| 25 |
| 4 |
根据菱形计算面积的公式,得
EC×BA=
| 1 |
| 2 |
即
| 25 |
| 4 |
| 1 |
| 2 |
解得EF=
| 15 |
| 2 |
点评:本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后对应边相等.同时,考查了勾股定理在折叠问题中的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
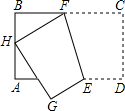 如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG=40°,则∠GEF的度数为( )
如图,将矩形纸片ABCD沿EF折叠,使得点C落在边AB上的点H处,点D落在点G处,若∠AHG=40°,则∠GEF的度数为( )| A、100° | B、110° | C、120° | D、135° |
 18、如图,将矩形纸片ABCD沿EF折叠后,点C、D分别落在点C′、D′处,若∠AFE=65°,则∠C′EF=
18、如图,将矩形纸片ABCD沿EF折叠后,点C、D分别落在点C′、D′处,若∠AFE=65°,则∠C′EF= 如图,将矩形纸片ABCD沿BD折叠,使点A落在点A′处,设A′B与CD相交于点E,若AB=8,BC=6,则EB=
如图,将矩形纸片ABCD沿BD折叠,使点A落在点A′处,设A′B与CD相交于点E,若AB=8,BC=6,则EB=