题目内容
1.解不等式组$\left\{\begin{array}{l}{2x+4>x+3①}\\{2x-1≤x+1②}\end{array}\right.$,并把解集在数轴上表示出来.分析 先分别解两个不等式得到x>-1和x≤2,然后根据大小小大中间找确定不等式组的解集,再利用数轴表示解集.
解答 解:解①得x>-1,
解②得x≤2,
所以不等式组的解集为-1<x≤2,
用数轴表示为: .
.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
9.下列各运算中,结果正确的是( )
| A. | 2$\sqrt{3}$+3$\sqrt{2}$=5$\sqrt{5}$ | B. | a8÷a2=a4 | C. | (-3a2)3=-27a6 | D. | (a2+b2)2=a4+b4 |
6.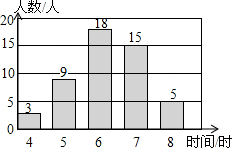 在开展“国学诵读”活动中,某校为了解1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制如图所示的条形统计图,根据图中数据,估计该校1300名学生一周的课外阅读时间不小于7小时的人数是( )
在开展“国学诵读”活动中,某校为了解1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制如图所示的条形统计图,根据图中数据,估计该校1300名学生一周的课外阅读时间不小于7小时的人数是( )
 在开展“国学诵读”活动中,某校为了解1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制如图所示的条形统计图,根据图中数据,估计该校1300名学生一周的课外阅读时间不小于7小时的人数是( )
在开展“国学诵读”活动中,某校为了解1300名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制如图所示的条形统计图,根据图中数据,估计该校1300名学生一周的课外阅读时间不小于7小时的人数是( )| A. | 600 | B. | 520 | C. | 130 | D. | 78 |
13. 如图,直线l1∥l2,∠1=55°,则∠2的度数是( )
如图,直线l1∥l2,∠1=55°,则∠2的度数是( )
 如图,直线l1∥l2,∠1=55°,则∠2的度数是( )
如图,直线l1∥l2,∠1=55°,则∠2的度数是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
10. 如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
 如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )| A. | 65° | B. | 80° | C. | 105° | D. | 115° |

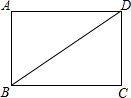 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.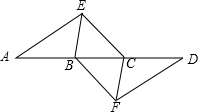 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.