题目内容
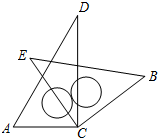 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°)
(1)若∠DCE=40°,则∠ACB的度数为
(2)若点E在AC的上方,设∠ACB=α(90°<α<180°),求∠DCE.(用含α的式子表示)
(3)请你动手操作,现将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C按顺时针方向任意转动一个角度,若0°<∠DCB<180°且点E在直线AC的上方,当这两块三角尺有一组边互相平行时,直接写出此时∠DCB角度所有可能的值(不必说明理由).
考点:角的计算
专题:
分析:(1)根据两角互余,可得∠ACE与∠DCE的关系,根据角的和差,可得答案;
(2)角的和差,可得∠ACE与∠ACB的关系,根据互余的两角的关系,可得∠DCE与∠ACE的关系,
(3)根据同位角、内错角、同旁内角的关系,可得答案.
(2)角的和差,可得∠ACE与∠ACB的关系,根据互余的两角的关系,可得∠DCE与∠ACE的关系,
(3)根据同位角、内错角、同旁内角的关系,可得答案.
解答:解:(1)由互余∠ACE=90°-∠DCE=90°-40°=50°,
由角的和差得∠ACB=∠ACE+∠BCE=50°+90°=140°;
(2)∠ACE=∠ACB-∠ECB=α-90°,
∠DCE=90°-∠ACE=90°-(α-90°)
=180°-α;
(3)∠DCBd的度数30°,45°,120°,135°;
故答案为:140°;180°-α;30°,45°,120°,135°.
由角的和差得∠ACB=∠ACE+∠BCE=50°+90°=140°;
(2)∠ACE=∠ACB-∠ECB=α-90°,
∠DCE=90°-∠ACE=90°-(α-90°)
=180°-α;
(3)∠DCBd的度数30°,45°,120°,135°;
故答案为:140°;180°-α;30°,45°,120°,135°.
点评:本题考查了角的计算,两角互余的性质,角的和差是解题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
下列各组中的两个单项式不属于同类项的是( )
| A、3m2n3和-m2n3 | ||
B、-1和
| ||
| C、a3和x3 | ||
D、-
|
下列说法正确的是( )
| A、延长射线OA到点B |
| B、线段AB为直线AB的一部分 |
| C、画一条直线,使它的长度为3cm |
| D、射线AB和射线BA是同一条射线 |
 用字母表示如图所示的阴影部分的面积是( )
用字母表示如图所示的阴影部分的面积是( )A、b(a+b)-
| ||
B、b(a+b)-
| ||
C、ab-
| ||
D、ab-
|
 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.