Question

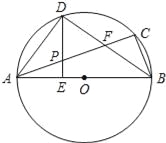
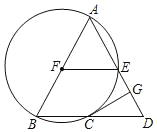
【题目】如图，在△ABD中，AB＝AD，以AB为直径的⊙F交BD于点C，交AD于E，CG是⊙F的切线，CG交AD于点G．

（1）求证：CG⊥AD；

（2）填空：

①若△BDA的面积为80，则△BCF的面积为　 　；

②当∠BAD的度数为　 　时，四边形EFCD是菱形．

Answer 1

【答案】（1）见解析；（2）①20；②60°

【解析】

（1）连接CF、AC，根据切线的性质得到CG⊥CF，再根据等腰三角形的性质得到∠B＝∠D，∠B＝∠BCF，故可知∠D＝∠BCF得到CF∥AD，故可证明CG⊥AD；

（2）①根据题意证明△BCF∽△BDA，利用即可求解；

②当∠BAD的度数为60°时，可得到△ABD、△AEF是等边三角形，得到EF是△ABD的中位线，各可证明四边形EFCD是平行四边形，再根据△BCF是等边三角形，得到EF＝CF，故可得到四边形EFCD是菱形.

（1）证明：连接CF、AC，如图所示：

∵CG是⊙F的切线，

∴CG⊥CF，

∵AB＝AD，BF＝CF，

∴∠B＝∠D，∠B＝∠BCF，

∴∠D＝∠BCF，

∴CF∥AD，

∴CG⊥AD；

（2）解：①∵AB为⊙F的直径，

∴∠ACB＝90°，

∴AC⊥BD，

∵AB＝AD，

∴BC＝CD＝BD，

∵CF∥AD，

∴△BCF∽△BDA，

∴，

∴，

∴S△BCF＝S△BDA＝×80＝20；

故答案为：20；

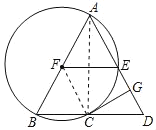
②当∠BAD的度数为60°时，四边形EFCD是菱形，理由如下：

∵AB＝AD，AF＝EF，∠BAD＝60°，

∴△ABD、△AEF是等边三角形，

∴AE＝EF＝AF＝BF＝AB＝AD，∠B＝60°，

∴AE＝DE，

∴EF是△ABD的中位线，

∴EF∥BD，EF＝BD＝CD，

∴四边形EFCD是平行四边形，

∵CF＝BF，

∴△BCF是等边三角形，

∴CF＝BF，

∴EF＝CF，

∴四边形EFCD是菱形；

故答案为：60°．