题目内容
甲、乙两台机床同时生产一种零件.在10天中,两台机床每天出次品的数量如下表:
(1)分别计算两组数据的平均数和方差;
(2)从计算的结果来看,在10天总,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
| 甲 | 1 | 1 | 0 | 2 | 1 | 3 | 2 | 1 | 1 | 0 |
| 乙 | 0 | 2 | 2 | 0 | 3 | 1 | 0 | 1 | 3 | 1 |
(2)从计算的结果来看,在10天总,哪台机床出次品的平均数较小?哪台机床出次品的波动较小?
考点:方差,加权平均数
专题:
分析:(1)根据平均数的计算公式先算出平均数,再根据方差公式进行计算即可;
(2)根据(1)得出的数据,进行比较,即可得出答案.
(2)根据(1)得出的数据,进行比较,即可得出答案.
解答:解:(1)甲的平均数是:(1+1+0+2+1+3+2+1+1+0)÷10=1.2;
乙的平均数是:(0+2+2+0+3+1+0+1+3+1)=1.3;
S2甲=
[5×(1-1.2)2+2×(0-1.2)2+2×(2-1.2)2+(3-1.2)2]=0.76;
S2乙=
[3×(0-1.3)2+2×(2-1.3)2+2×(3-1.3)2+3×(1-1.3)2]=1.21;
(2)∵
甲=1.2,
乙=1.3,
∴乙机床出次品的平均数较小;
∵S2甲=0.76,S2乙=1.215,
∴S2甲<S2乙,
∴甲机床出次品的波动较小.
乙的平均数是:(0+2+2+0+3+1+0+1+3+1)=1.3;
S2甲=
| 1 |
| 10 |
S2乙=
| 1 |
| 10 |
(2)∵
. |
| x |
. |
| x |
∴乙机床出次品的平均数较小;
∵S2甲=0.76,S2乙=1.215,
∴S2甲<S2乙,
∴甲机床出次品的波动较小.
点评:此题考查了平均数和方差,一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图图形是按一定的规律排列的,依照此规律,第10个图形有( )条线段.


| A、125 | B、140 |
| C、155 | D、160 |
 如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )
如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )| A、∠M=∠N |
| B、AB=CD |
| C、AM∥CN |
| D、AM=CN |
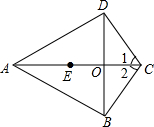 如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC. 在长形花坛ABCD中,P、Q两处是凉亭,要在花坛内建一个喷水池O,使O到AB、AD的距离相等,且到凉亭P、Q的距离也相等.
在长形花坛ABCD中,P、Q两处是凉亭,要在花坛内建一个喷水池O,使O到AB、AD的距离相等,且到凉亭P、Q的距离也相等. 如图,10×10的方格纸的两条对称轴a、b相交于点O,△ABC的顶点均在格点上.
如图,10×10的方格纸的两条对称轴a、b相交于点O,△ABC的顶点均在格点上.