题目内容
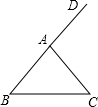如图，三角形ABC中，AB=AC，外角∠CAD=100°，求∠B的度数．
解：∵AB=AC，
∴∠B=∠C．
∵∠CAD=∠B+∠C=2∠B=100°．
∴∠B=50°．
分析：欲求∠B的度数，根据已知可判断∠A是三角形的顶角，根据已知可利用三角形外角及等腰三角形性质求解．
点评：本题考查了等腰三角形的性质与三角形内、外角的关系等知识；利用外角得到∠CAD=2∠B是正确解答本题的关键．
∴∠B=∠C．
∵∠CAD=∠B+∠C=2∠B=100°．
∴∠B=50°．
分析：欲求∠B的度数，根据已知可判断∠A是三角形的顶角，根据已知可利用三角形外角及等腰三角形性质求解．
点评：本题考查了等腰三角形的性质与三角形内、外角的关系等知识；利用外角得到∠CAD=2∠B是正确解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
16、如图，三角形ABC中，∠C=90°，它的三边AB、AC、BC中，
15、如图，三角形ABC中任意一点P（x，y），经过平移后对应的点Q（x+5，y+3），将三角形ABC作同样的平移到三角形A1B1C1．
已知：如图等腰三角形ABC中，AB=AC，BD平分∠ABC交AC于D，若∠BDC=78°，求∠C的度数？
如图，三角形ABC中，顶点B的位置表示为（1，2），点A的位置表示为（2，4）．则点C表示位置为
画图并计算，在如图的三角形ABC中：