题目内容
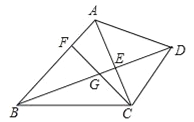
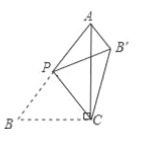
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的动点(不与点
边上的动点(不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在直线翻折,得到
所在直线翻折,得到![]() ,连接
,连接![]() , 则下面结论错误的是( )
, 则下面结论错误的是( )
A.当![]() 时,
时,![]()
B.当![]() 时,∠
时,∠![]()
C.当 ![]() 时,
时,![]()
D.![]() 长度的最小值是1
长度的最小值是1
【答案】C
【解析】
A.根据折叠性质和三角形内角和定理可证∠ABP=∠CPB,从而可证![]() ;
;
B.根据折叠性质和直角三角形斜边上的中线等于斜边的一半可知PA=PB=PC=PB,A、B、C、B四点共圆,根据圆周角定理即可求出![]() ;
;
C.根据相似三角形的判定证得△PAC∽△CAB,再根据相似三角形的对应边成比例求得AP的值,即可判断![]() 错误;
错误;
D. 根据两点之间线段最短,求得![]() 长度的最小值,即可判断此结论正确.
长度的最小值,即可判断此结论正确.
在△ABC中,∠ACB=90°,AP=BP,
∴AP=BP=CP,∠BPC=![]()
由折叠的性质可得
CP=BP,∠CPB=∠BPC=![]()
∴AP=BP,
∴∠ABP=∠BAP=![]()
∴∠ABP=∠CPB
∴AB//CP
故A正确;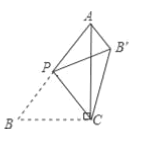
∵AP=BP,
∴PA=PB=PC=PB,
∴点A,B,C,B在以点P为圆心,PA长为半径的圆上
由折叠的性质可得BC=BC,
∴![]()
∴∠BPC=2∠BAC
故B正确;
当CP⊥AB时,∠APC=∠ACB
∵∠PAC=∠CAB
∴△PAC∽△CAB
∴![]()
∵在Rt△ABC中,AC=![]()
∴AP=![]()
故C错误;
由轴对称的性质可知:
BC=CB=3
∵CB长度固定不变,
∴当AB+CB有最小值时,AB的长度有最小值
根据两点之间线段最短可知:
当A、B、C三点在一条直线上时,AB有最小值,
∴AB=AC-BC=4-3=1
故D正确
故选:C

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目