题目内容
如图,在等边△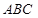 中,
中,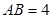 ,当直角三角板
,当直角三角板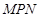 的
的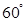 角的顶点
角的顶点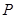 在
在 上移动时,斜边
上移动时,斜边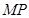 始终经过
始终经过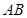 边的中点
边的中点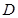 ,设直角三角板的另一直角边
,设直角三角板的另一直角边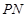 与
与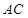 相交于点E.设
相交于点E.设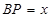 ,
,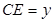 ,那么
,那么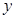 与
与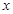 之间的函数图象大致是( )
之间的函数图象大致是( )
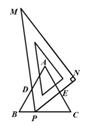
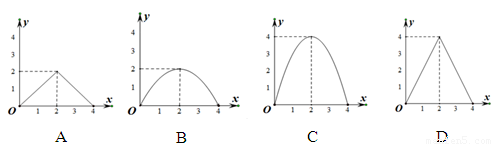
【答案】
B.
【解析】
试题分析:根据等边三角形的性质得BD=2,PC=4-x,∠B=∠C=60°,由于∠MPN=60°,易得∠DPB=∠PEC,根据三角形相似的判定方法得到△BPD∽△CEP,利用相似比即可得到y=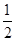 x(4-x),配方得到y=-
x(4-x),配方得到y=-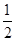 (x-2)2+2,然后根据二次函数的性质对各选项进行判断.
(x-2)2+2,然后根据二次函数的性质对各选项进行判断.
∵等边△ABC中,AB=4,BP=x,
∴BD=2,PC=4-x,∠B=∠C=60°,
∵∠MPN=60°,
∴∠DPB+∠EPC=120°,
∵∠EPC+∠PEC=120°,
∴∠DPB=∠PEC,
∴△BPD∽△CEP,
∴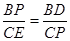 ,即
,即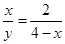 ,
,
∴y=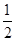 x(4-x)=-
x(4-x)=-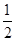 (x-2)2+2,(0≤x≤4).
(x-2)2+2,(0≤x≤4).
故选B.
考点: 动点问题的函数图象.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在等边△ABC中,D、E、F分别是BC,AC,AB上的点,且DE⊥AC,EF⊥AB,FD⊥BC,则△DEF与△ABC的面积之比等于( )
如图,在等边△ABC中,D、E、F分别是BC,AC,AB上的点,且DE⊥AC,EF⊥AB,FD⊥BC,则△DEF与△ABC的面积之比等于( )| A、1:3 | ||
| B、2:3 | ||
C、
| ||
D、
|
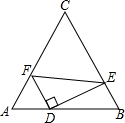 如图.在等边△ABC中,AC=8,点D、E、F分别在三边AB、BC、AC上,且AF=2,FD⊥DE,∠DFE=60°,则AD的长为
如图.在等边△ABC中,AC=8,点D、E、F分别在三边AB、BC、AC上,且AF=2,FD⊥DE,∠DFE=60°,则AD的长为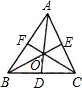 如图,在等边△ABC中,D、E、F是三边中点.在图中可以数出的三角形中,任选一对三角形(不计顺序),如果这2个三角形至少有一条边相等,便称之为一对“友好三角形”.那么,从图中选出“友好三角形”共有( )
如图,在等边△ABC中,D、E、F是三边中点.在图中可以数出的三角形中,任选一对三角形(不计顺序),如果这2个三角形至少有一条边相等,便称之为一对“友好三角形”.那么,从图中选出“友好三角形”共有( ) 如图,在等边△ABC中,D在BC边上,E在△ABC外,∠BAD=15°,∠DAE=70°,AD=AE,求∠CAE,∠EDC,∠EFC的度数.
如图,在等边△ABC中,D在BC边上,E在△ABC外,∠BAD=15°,∠DAE=70°,AD=AE,求∠CAE,∠EDC,∠EFC的度数. 如图,在等边△ABC中,AD⊥BC,AB=5cm,则DC的长为
如图,在等边△ABC中,AD⊥BC,AB=5cm,则DC的长为