题目内容
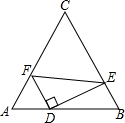 如图.在等边△ABC中,AC=8,点D、E、F分别在三边AB、BC、AC上,且AF=2,FD⊥DE,∠DFE=60°,则AD的长为
如图.在等边△ABC中,AC=8,点D、E、F分别在三边AB、BC、AC上,且AF=2,FD⊥DE,∠DFE=60°,则AD的长为3
3
.分析:根据三角形的内角和定理列式求出∠2=∠3,再根据等边三角形的三个角都是60°求出∠A=∠C,然后根据两组角对应相等的两个三角形相似求出△ADF和△CFE相似,根据相似三角形对应边成比例可得
=
,再根据直角三角形30°角所对的直角边等于斜边的一半可得DF=
EF,然后代入数据进行计算即可得解.
| AD |
| CF |
| DF |
| EF |
| 1 |
| 2 |
解答: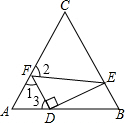 解:∵∠DFE=60°,
解:∵∠DFE=60°,
∴∠1+∠2+60°=180°,
∴∠2=120°-∠1,
在等边△ABC中,∠A=∠C=60°,
∴∠A+∠1+∠3=180°,
∴∠3=180°-∠A-∠1=120°-∠1,
∴∠2=∠3,
又∵∠A=∠C,
∴△ADF∽△CFE,
∴
=
,
∵FD⊥DE,∠DFE=60°,
∴∠DEF=90°-60°=30°,
∴DF=
EF,
又∵AF=2,AC=8,
∴CF=8-2=6,
∴
=
,
解得AD=3.
故答案为:3.
 解:∵∠DFE=60°,
解:∵∠DFE=60°,∴∠1+∠2+60°=180°,
∴∠2=120°-∠1,
在等边△ABC中,∠A=∠C=60°,
∴∠A+∠1+∠3=180°,
∴∠3=180°-∠A-∠1=120°-∠1,
∴∠2=∠3,
又∵∠A=∠C,
∴△ADF∽△CFE,
∴
| AD |
| CF |
| DF |
| EF |
∵FD⊥DE,∠DFE=60°,
∴∠DEF=90°-60°=30°,
∴DF=
| 1 |
| 2 |
又∵AF=2,AC=8,
∴CF=8-2=6,
∴
| AD |
| 6 |
| 1 |
| 2 |
解得AD=3.
故答案为:3.
点评:本题考查了相似三角形的判定与性质,等边三角形的性质,直角三角形30°角所对的直角边等于斜边的一半,根据平角等于180°和三角形的内角和定理求出∠2=∠3是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
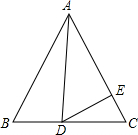 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: