��Ŀ����
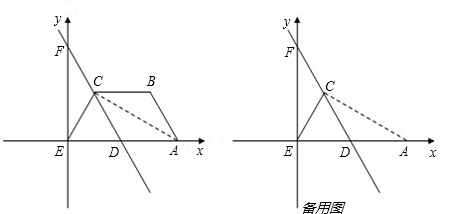
��ͼ���ڵ�������ABCE�У�BC��AE��AB=BC���Ե�EΪ����ԭ�㽨��ƽ��ֱ������ϵ����������ABCD��AC�۵���ʹ��Bǡ������x���ϵ�Dλ�ã���C��D�����ֱ����y�ύ�ڵ�F����1�����ж��ı���ABCD�������������ı��Σ���˵��������ɣ�
��2�������BAE=60�㣬AB=2cm����ô��y�����Ƿ����һ��P��ʹ��P��D��FΪ����������ι��ɵ��������Σ������ڣ���������п��ܵ�P�����꣬�������ڣ���˵�����ɣ�
��3���ڣ�2���������£�������EDF��x����������1cm/s���ٶ�ƽ�Ƶ���E���A�غ�ʱΪֹ�����EDF��ƽ�ƹ��������ECA�غϲ��ֵ����ΪS��ƽ�Ƶ�ʱ��Ϊx�룬�����S��x֮��ĺ�����ϵʽ���Ա�����Χ���������ʱS�����ֵ�����ֵ�Ƕ��٣�
��������1������֪��AB=BC=DA=AB�������ı���ABCDΪ���Σ�
��2������PDF����������DF����Ϊ�����ֱ������ҳ����ϵ�������������жϣ�
��3���ɣ�2���ɵã�AE=DE+AD=4cm����DE=2��AD=2�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��E��M=
x��AD'=AE-D��E��-EE'=4-2-x=2-x���ɵ�S��EME��=
x2��S��AD��N=
��2-x��2����S=S��ADE-S��EME��-S��AD��N�����������ɵ�S��x�Ľ���ʽ�����ݶ��κ���������������ֵ���ɣ�
��2������PDF����������DF����Ϊ�����ֱ������ҳ����ϵ�������������жϣ�
��3���ɣ�2���ɵã�AE=DE+AD=4cm����DE=2��AD=2�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��E��M=
| 3 |
| ||
| 2 |
| ||
| 4 |
����⣺��1���ı���ABCDΪ���Σ�
�������£���Ϊ��B�͵�D����ֱ��AC�Գ�����AB=AD��BC=DC����AB=BC��AB=BC=DA=AB�������ı���ABCDΪ���Σ�
��2����Ϊ�ı���ABCDΪ���Σ�����DF��AB�����ԡ�CDE=��CED=60�㣬���ԡ�CDEΪ�ȱ������Σ�����DE=CD=AB=2cm����Rt��DEF�У�DF=DEcos60��=2cos60��=4cm��
�������FΪ���㣬��FP=FDʱ��P������Ϊ��0��4+2
������0��2
-4����
�������PΪ���㣬��PF=PDʱ��P������Ϊ��0��
����
�������DΪ���㣬��DF=DPʱ��P������Ϊ��0��-2
����
����������P��������0��4+2
������0��2
-4������0��
������0��-2
����
��3��

�ɣ�2���ɵã�AE=DE+AD=4cm����DE=2��AD=2
�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��E��A=4-x��AD'=AE��-E��D��=4-x-2=2-x��
�ɵ�S��A��ME��=
��4-x��2��S��AD��N=
��2-x��2��
��S=S��A��ME��-S��AD��N=
��4-x��2-
��2-x��2��0��x��1����

�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��E��M=
x��AD'=AE-D'E��-EE��=4-2-x=2-x
�ɵ�S��EME��=
x2
S��AD��N=
��2-x��2��
��S=S��AME-S��EME��-S��AD��N=
��2��2
-
x2-
��2-x��2=-
x2+
x+
��1��x��2��
��x=-
=-
=
����x=1ʱ��S�����ֵ�ǣ�
��2-1��2=
��
�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��AE��=4-x��
�ɵ�S=S��A��ME��=
��4-x��2��2��x��4����

�������£���Ϊ��B�͵�D����ֱ��AC�Գ�����AB=AD��BC=DC����AB=BC��AB=BC=DA=AB�������ı���ABCDΪ���Σ�
��2����Ϊ�ı���ABCDΪ���Σ�����DF��AB�����ԡ�CDE=��CED=60�㣬���ԡ�CDEΪ�ȱ������Σ�����DE=CD=AB=2cm����Rt��DEF�У�DF=DEcos60��=2cos60��=4cm��
�������FΪ���㣬��FP=FDʱ��P������Ϊ��0��4+2
| 3 |
| 3 |
�������PΪ���㣬��PF=PDʱ��P������Ϊ��0��
2
| ||
| 3 |
�������DΪ���㣬��DF=DPʱ��P������Ϊ��0��-2
| 3 |
����������P��������0��4+2
| 3 |
| 3 |
2
| ||
| 3 |
| 3 |
��3��

�ɣ�2���ɵã�AE=DE+AD=4cm����DE=2��AD=2
�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��E��A=4-x��AD'=AE��-E��D��=4-x-2=2-x��
�ɵ�S��A��ME��=
| ||
| 6 |
| ||
| 4 |
��S=S��A��ME��-S��AD��N=
| ||
| 6 |
| ||
| 4 |

�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��E��M=
| 3 |
�ɵ�S��EME��=
| ||
| 2 |
S��AD��N=
| ||
| 4 |
��S=S��AME-S��EME��-S��AD��N=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
��x=-
| b |
| 2a |
| ||||
2��(-
|
| 2 |
| 3 |
| ||
| 4 |
| ||
| 4 |
�����DEFƽ�Ƶ���D��E��F�䣬��EE��=x��AE��=4-x��
�ɵ�S=S��A��ME��=
| ||
| 6 |

���������⿼�����Σ����Ρ�ֱ�������Ρ����κ��������֪ʶ�����⼰���ã��ۺ���ǿ������ʱҪע��֪ʶ��֮�����ϵ��

��ϰ��ϵ�д�
�����Ŀ
 �ڣ����������t��ֵ���������ڣ���˵�����ɣ�
�ڣ����������t��ֵ���������ڣ���˵�����ɣ� 10����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC��EΪAD���е㣬��֤��BE=CE��
10����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC��EΪAD���е㣬��֤��BE=CE�� ��֪����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC����E��F�ֱ���AB��DC�ϣ���BE=3EA��CF=3FD��
��֪����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC����E��F�ֱ���AB��DC�ϣ���BE=3EA��CF=3FD�� ��2012•���ݣ���ͼ���ڵ�������ABCD�У�BC��AD��AD=5��DC=4��DE��AB��BC�ڵ�E����EC=3��������ABCD���ܳ��ǣ�������
��2012•���ݣ���ͼ���ڵ�������ABCD�У�BC��AD��AD=5��DC=4��DE��AB��BC�ڵ�E����EC=3��������ABCD���ܳ��ǣ������� ����
����