题目内容
已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.

(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕点O旋转时,∠DOE的大小是否发生变化?若变化,说明理由;若不变,求∠DOE的度数.
(1)45°;(2),不变,∠DOE=45°
【解析】
试题分析:根据角平分线的性质可以得到∠BOC=2∠COE,∠AOC=2∠DOC,再根据∠AOC+∠BOC=90°就可以得出∠DOE的度数.
试题解析:(1)∵OD、OE分别平分∠AOC和∠BOC.
∴∠COE= ∠COB=35°, ∠COD=
∠COB=35°, ∠COD= ∠AOC=15°
∠AOC=15°
∴∠DOE=∠DOC+∠EOC= 45°
(2) ∠DOE的大小不变等于45°
理由:∠DOE= ∠DOC+∠COE= ∠A OC+
∠A OC+ ∠COB=
∠COB= (∠AOC+∠ COB)=
(∠AOC+∠ COB)= ∠AOB=45°
∠AOB=45°
考点:角平分线的性质

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
雷霆队的杜兰特当选为2013﹣2014赛季NBA常规赛MVP,下表是他8场比赛的得分,则这8场比赛得分的众数与中位数分别为( )
场次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
得分 | 30 | 28 | 28 | 38 | 23 | 26 | 39 | 42 |
A.28 29 B.29 28 C.28 28 D.28 27
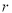 米,广场长为
米,广场长为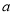 米,宽为
米,宽为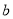 米。
米。
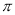 )。
)。 -(3x-5y) +[ 4
-(3x-5y) +[ 4 -(3
-(3 ,y=-
,y=- .
.
 B.
B. C.
C. D.
D.