题目内容
7. 如图,已知Rt△ABC中,∠C=90°,AC=8.BC=6,点P以每秒1个单位的速度从
如图,已知Rt△ABC中,∠C=90°,AC=8.BC=6,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都
停止运动,设点P、Q运动的时间为t秒.
(Ⅰ)在运动过程中,请你用t表示P、Q两点间的距离,并求出P、Q两点间的距离
的最大值;
(Ⅱ)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式.
分析 (Ⅰ)分Q在AB边上与Q在BC边上,分别如图1和图2所示,表示出PQ的长,当Q与B重合时,PQ取得最大值,求出即可;
(Ⅱ)分两种情况考虑:当Q在AB边上时,如图1,△ABC被直线PQ扫过的面积为S△AQP;当Q在BC边上时,△ABC被直线PQ扫过的面积为S四边形ABQP,分别表示出S与t的函数关系式即可.
解答 解:(Ⅰ)分两种情况考虑:
当Q在AB边上时,过Q作QE⊥AC,交AC于点E,连接PQ,如图1所示: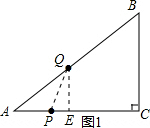
∵∠C=90°,
∴QE∥BC,
∴△ABC∽△AQE,
∴$\frac{AQ}{AB}$=$\frac{AE}{AC}$=$\frac{QE}{BC}$,
在Rt△ABC中,AC=8,BC=6,
根据勾股定理得:AB=10,
∵AQ=2t,AP=t,
∴$\frac{2t}{10}$=$\frac{t+PE}{8}$=$\frac{QE}{6}$,
整理得:PE=$\frac{3}{5}$t,QE=$\frac{6}{5}$t,
根据勾股定理得:PQ2=QE2+PE2,
整理得:PQ=$\frac{3\sqrt{5}}{5}$t;
当Q在BC边上时,连接PQ,如图2所示: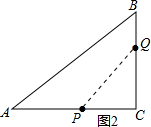
由AB+BQ=2t,AB=10,得到BQ=2t-10,CQ=BC-BQ=6-(2t-10)=16-2t,
由AP=t,AC=8,得到PC=8-t,
根据勾股定理得:PQ=$\sqrt{P{C}^{2}+Q{C}^{2}}$=$\sqrt{(16-2t)^{2}+(8-t)^{2}}$,
当Q与B重合时,PQ的值最大,
则当t=5时,PQ最大值为3$\sqrt{5}$;
(Ⅱ)分两种情况考虑:
当Q在AB边上时,如图1,△ABC被直线PQ扫过的面积为S△AQP,
此时S=$\frac{1}{2}$AP•QE=$\frac{1}{2}$t•$\frac{6}{5}$t=$\frac{3}{5}$t2(0<t≤5);
当Q在BC边上时,△ABC被直线PQ扫过的面积为S四边形ABQP,
此时S=S△ABC-S△PQC=$\frac{1}{2}$×8×6-$\frac{1}{2}$(8-t)(16-2t)=-t2+16t-40(5<t≤8).
综上,经过t秒的运动,△ABC被直线PQ扫过的面积S与时间t的函数关系式为$\left\{\begin{array}{l}{s=\frac{3}{5}{t}^{2}(0<t≤5)}\\{s=-{t}^{2}+16t-40(5<t≤8)}\end{array}\right.$.
点评 此题考查了动点问题的函数图象,涉及的知识有:相似三角形的判定与性质,勾股定理,以及三角形面积求法,利用了分类讨论的思想,分类讨论时考虑问题要全面,做到不重不漏.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案

 已知,平行四边形ABCD中,点E在DC边上,且DE=3EC,AC与BE交于点F;
已知,平行四边形ABCD中,点E在DC边上,且DE=3EC,AC与BE交于点F; 如图,在△ABC中,OB,OC分别是∠ABC,∠ACB的平分线,OM∥BC,分别交AB,AC于点M,N.若MB=8,NC=6,则MN的长是( )
如图,在△ABC中,OB,OC分别是∠ABC,∠ACB的平分线,OM∥BC,分别交AB,AC于点M,N.若MB=8,NC=6,则MN的长是( ) 如图,直线y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于A(1,6),B(a,3)两点.
如图,直线y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于A(1,6),B(a,3)两点.