题目内容
如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B.若∠ABP=33°,则∠P= °.
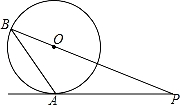
24 °.
【考点】切线的性质.
【分析】连接OA,根据切线的性质得出OA⊥AP,利用圆心角和圆周角的关系解答即可.
【解答】解:连接OA,如图:

∵PA是⊙O的切线,切点为A,
∴OA⊥AP,
∴∠OAP=90°,
∵∠ABP=33°,
∴∠AOP=66°,
∴∠P=90°﹣66°=24°.
故答案为:24.
【点评】此题考查切线的性质,关键是根据切线的性质得出OA⊥AP,再利用圆心角和圆周角的关系解答.

练习册系列答案
相关题目
 ,则
,则 :
: .
. 等于( )
等于( )
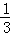 B.
B.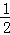 C.
C. D.
D.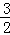
 (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .
(k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .

 向右平移1个单位,再向上平移2个单位后所得到抛物线为( )
向右平移1个单位,再向上平移2个单位后所得到抛物线为( ) B. y =
B. y = 
 D.y=
D.y=