题目内容
2.已知在等腰直角三角形ABC中,∠BAC=90°,AB=AC=4,将边AB绕着点A旋转至AB′位置,且AB′与AC边之间的夹角为30°,那么线段BB′的长等于4或4$\sqrt{3}$.分析 分类讨论:如图1,∠B′AC=30°,则∠BAB′=60°,由旋转的性质得AB=AB′,则可判断△ABB′为等边三角形,于是有BB′=AB=4;如图2,∠B′AC=30°,则∠BAB′=120°,再由旋转的性质得AB=AB′=4,根据等腰三角形的性质和三角形内角和定理可得∠ABB′=∠AB′B=30°,作AH⊥BB′于H,根据等腰三角形的性质得BH=B′H,然后在Rt△ABH中利用含30度的直角三角形三边的关系可计算出BH=2$\sqrt{3}$,于是得到BB′=2BH=4$\sqrt{3}$
解答 解:如图1,∠B′AC=30°,
∵∠BAC=90°,
∴∠BAB′=60°
即边AB绕着点A顺时针旋转60°至AB′位置,
∴AB=AB′,
∴△ABB′为等边三角形,
∴BB′=AB=4;
如图2,∠B′AC=30°,
∵∠BAC=90°,
∴∠BAB′=120°
即边AB绕着点A顺时针旋转60°至AB′位置,
∴AB=AB′=4,
∴∠ABB′=∠AB′B=30°,
作AH⊥BB′于H,则BH=B′H,
在Rt△ABH中,∵∠ABH=30°,
∴AH=$\frac{1}{2}$BA=2,
BH=$\sqrt{3}$AH=2$\sqrt{3}$,
∴BB′=2BH=4$\sqrt{3}$,
综上所述,BB′的长为4或4$\sqrt{3}$.
故答案为4或4$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.运用分类讨论的思想是解决本题的关键.

练习册系列答案
相关题目
19.某水果公式销售人员从所有柑橘中随机抽取若干柑橘进行“柑橘损坏率”统计,结果如下表:
估计这种柑橘损坏的概率约为0.1(精确到0.1)
| 柑橘总质量(n) | 损坏柑橘质量(m) | 柑橘损坏率(m/n) |
| 400 | 39.24 | 0.098 |
| 450 | 44.57 | 0.099 |
| 500 | 51.54 | 0.103 |
11.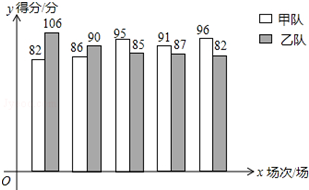 甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
(1)请根据统计图填写下表
(2)如果从两队中选派一支球队参加篮球锦标赛,根据上述统计,从平均分、方差以及获胜场数这三个方面分别进行简要分析,你认为选派哪支球队参赛更能取得好成绩?
 甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)
甲乙两支篮球队进行了5场比赛,比赛成绩绘制成了统计图(如图)(1)请根据统计图填写下表
| 平均数 | 中位数 | 方差 | |
| 甲 | 90 | 91 | 28.4 |
| 乙 | 90 | 87 | 70.8 |
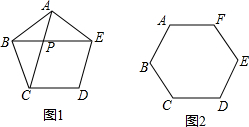
 如图,AB∥CD,∠A=∠D=60°,AC与BD交于点E,连接BC,其中点M,N,K 分别是AE,BC,DE边上的中点.求证:NK=MN.
如图,AB∥CD,∠A=∠D=60°,AC与BD交于点E,连接BC,其中点M,N,K 分别是AE,BC,DE边上的中点.求证:NK=MN.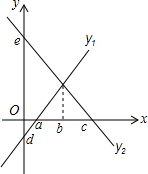 如图,先观察图形,然后填空:
如图,先观察图形,然后填空: 在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第5次碰到矩形的边时,点P的坐标为(1,4);当点P第2016次碰到矩形的边时,点P的坐标为(0,3).
在平面直角坐标系xOy中,矩形OABC如图放置,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第5次碰到矩形的边时,点P的坐标为(1,4);当点P第2016次碰到矩形的边时,点P的坐标为(0,3).