题目内容
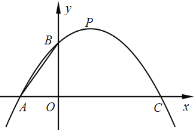
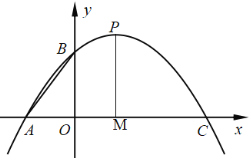
【题目】如图,二次函数![]() (a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(a 0) 与 x 轴交于 A、C 两点,与 y 轴交于点 B,P 为 抛物线的顶点,连接 AB,已知 OA:OC=1:3.
(1)求 A、C 两点坐标;
(2)过点 B 作 BD∥x 轴交抛物线于 D,过点 P 作 PE∥AB 交 x 轴于 E,连接 DE,
①求 E 坐标;
②若 tan∠BPM=![]() ,求抛物线的解析式.
,求抛物线的解析式.
【答案】(1)A(-1,0),C(3,0);(2)① E(-![]() ,0);②原函数解析式为:
,0);②原函数解析式为:![]() .
.
【解析】
(1)由二次函数的解析式可求出对称轴为x=1,过点P作PE⊥x轴于点E,所以设A(-m,0),C(3m,0),结合对称轴即可求出结果;
(2) ①过点P作PM⊥x轴于点M,连接PE,DE,先证明△ABO![]() △EPM得到
△EPM得到![]() ,找出OE=
,找出OE=![]() ,再根据A(-1,0)代入解析式得:3a+c=0,c=-3a,即可求出OE的长,则坐标即可找到;
,再根据A(-1,0)代入解析式得:3a+c=0,c=-3a,即可求出OE的长,则坐标即可找到;
②设PM交BD于点N;根据点P(1,c-a),BN‖AC,PM⊥x轴表示出PN=-a,再由tan∠BPM=![]() 求出a,结合(1)知道c,即可知道函数解析式.
求出a,结合(1)知道c,即可知道函数解析式.
(1)∵二次函数为:![]() (a<0),
(a<0),
∴对称轴为![]() ,
,
过点P作PM⊥x轴于点M,
则M(1,0),M为AC中点,
又OA:OC=1:3,
设A(-m,0),C(3m,0),
∴![]() ,
,
解得:m=1,
∴A(-1,0),C(3,0),
(2)①做图如下:
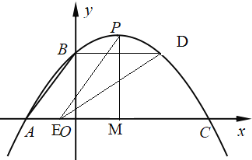
∵PE∥AB,
∴∠BAO=∠PEM,
又∠AOB=∠EMP,
∴△ABO![]() △EPM,
△EPM,
∴![]() ,
,
由(1)知:A(-1,0),C(3,0),M(1,0),B(0,c),P(1,c-a),
∴![]() ,
,
∴OE=![]() ,
,
将A(-1,0)代入解析式得:3a+c=0,
∴c=-3a,
∴![]() ,
,
∴E(-![]() ,0);
,0);
②
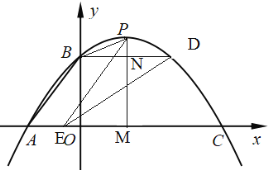
设PM交BD于点N;
∵![]() (a<0),
(a<0),
∴x=1时,y=c-a,即点P(1,c-a),
∵BN‖AC,PM⊥x轴
∴NM= BO=c,BN=OM=1,
∴PN=-a,
∵tan∠BPM=![]() ,
,
∴tan∠BPM=![]() ,
,
∴PN=![]() ,
,
即a=-![]() ,
,
由(1)知c=-3a,
∴c=![]() ;
;
∴原函数解析式为:![]() .
.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案