题目内容
 为了提高技术工人的技能技巧,某石油分公司举办了一期岗位培训班,培训结业时出了如下一道题:有一油罐,其直径为6米,高8米,如图,将一长为12米的金属棒置于其中,假如金属棒在外面的长为h米,试问h的取值范围是( )
为了提高技术工人的技能技巧,某石油分公司举办了一期岗位培训班,培训结业时出了如下一道题:有一油罐,其直径为6米,高8米,如图,将一长为12米的金属棒置于其中,假如金属棒在外面的长为h米,试问h的取值范围是( )分析:根据杯子内金属棒的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
解答:解:∵将一根长为12m的金属棒,置于底面直径为6m,高为8m的圆柱形水杯中,
∴在杯子中的金属棒最短等于杯子的高,最长等于金属棒、杯子直径和杯子的高构成的直角三角形斜边的长,
∴当杯子中金属棒最短等于杯子的高,即l=8m,
最长等于金属棒、杯子直径和杯子的高构成的直角三角形斜边的长,即l=
=10m
∴h的取值范围是:(12-10)≤h≤(12-8),即2≤h≤4.
故选:D.
∴在杯子中的金属棒最短等于杯子的高,最长等于金属棒、杯子直径和杯子的高构成的直角三角形斜边的长,
∴当杯子中金属棒最短等于杯子的高,即l=8m,
最长等于金属棒、杯子直径和杯子的高构成的直角三角形斜边的长,即l=
| 82+62 |
∴h的取值范围是:(12-10)≤h≤(12-8),即2≤h≤4.
故选:D.
点评:此题主要考查了勾股定理的应用,根据题意构造出直角三角形是解答此题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
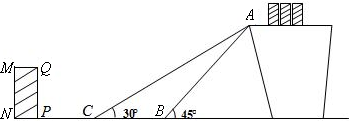
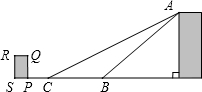
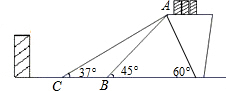 过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°成为37°,因此传送带的落地点B到点C向前移动了2米.
过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°成为37°,因此传送带的落地点B到点C向前移动了2米. 为提高技术工人的技能技巧,某石油分公司举办了一期岗位培训班.培训结业时出了如下一道试题:有一油罐,其直径为6米,高为8米,如图,将一长为12米的金属棒置于其中,假如金属棒露在外面的长为h米,试问h的取值范围是________.
为提高技术工人的技能技巧,某石油分公司举办了一期岗位培训班.培训结业时出了如下一道试题:有一油罐,其直径为6米,高为8米,如图,将一长为12米的金属棒置于其中,假如金属棒露在外面的长为h米,试问h的取值范围是________.