题目内容
10.如图,在平面直角坐标系中,点O为坐标原点,A点的坐标为(3,0),以OA为边作等边三角形OAB,点B在第一象限,过点B作AB的垂线交x轴于点C.动点P从O点出发沿OC向C点运动,动点Q从B点出发沿BA向A点运动,P,Q两点同时出发,速度均为1个单位/秒.设运动时间为t秒.(Ⅰ)求线段BC的长;
(Ⅱ)如图①,连接PQ交线段OB于点E,过点E作x轴的平行线交线段BC于点F.设线段EF的长为m,求m与t之间的函数关系式,并直接写出自变量t的取值范围:
(Ⅲ)如图②,在(Ⅱ)的条件下,将△BEF绕点B逆时针旋转得到△BE′F′,使点E的对应点E′落在线段AB上,点F的对应点是F′,E′F′交x轴于点G,连接PF、QG,当PF=t时,直接写出QG的长(不需写出解题过程).
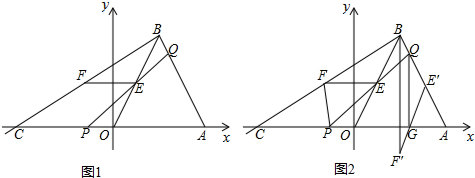
分析 (1)先根据等边三角形得出AB=OA=3,再根据含30°的直角三角形的性质得出BC的长;
(2)过点Q作QN∥OB交x轴于点N,再根据等边三角形的性质证明△POE和△PNQ相似,根据相似三角形得出对应边关系,得出函数关系式即可;
(3)根据PF=t,此时EF=t,得出QG的长度即可.
解答 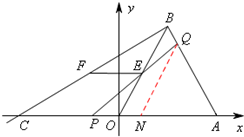 解:(Ⅰ)∵△AOB为等边三角形,
解:(Ⅰ)∵△AOB为等边三角形,
∴∠BAC=∠AOB=60°,
∵BC⊥AB,∠ABC=90°,
∴∠ACB=30°,∠OBC=30°,∠ACB=∠OBC,
∴CO=OB=AB=OA=3,
∴AC=6,
∴BC=$\sqrt{A{C^2}-A{B^2}}=\sqrt{{6^2}-{3^2}}$=$3\sqrt{3}$;
(Ⅱ)如图,过点Q作QN∥OB交x轴于点N,
∴∠QNA=∠BOA=60°=∠QAN,
∴△AQN为等边三角形,
∵BQ=t,
∴NQ=NA=AQ=3-t,
∴ON=3-(3-t)=t,
∴PN=t+t=2t,
∵OE∥QN,
∴△POE∽△PNQ,
∴$\frac{OE}{NQ}=\frac{PO}{PN}$,
即$\frac{OE}{3-t}=\frac{t}{2t}$,
∴$OE=\frac{3}{2}-\frac{1}{2}t$,
∵EF∥x轴,
∴∠BFE=∠BCO=∠FBE=30°,
∴EF=BE,
∴$m=BE=OB-OE=3-(\frac{3}{2}-\frac{1}{2}t)=\frac{1}{2}t+\frac{3}{2}$(0<t<3),
(Ⅲ)∵△BEF绕点B逆时针旋转得到△BE′F′,
∴∠F′BE′=30°,
当PF=t时,EF=t,
可得:t=1,
∴AQ=2,AG=1,
可得:$QG=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
点评 此题考查几何变换问题,关键是根据等边三角形的性质分析问题,同时也利用了相似三角形的判定和性质解答.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案 在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}a{x^2}$+2x-a+1与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}a{x^2}$+2x-a+1与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.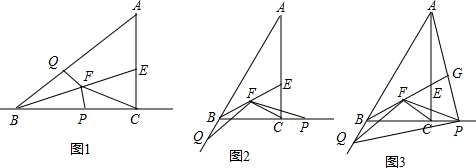
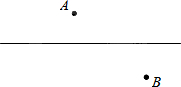 如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?
如图,在公路l的两旁有两个工厂A、B,要在公路上搭建一个货场让A、B两厂使用,要使货场到A、B两厂的距离之和最小,问货场应建在什么位置?为什么?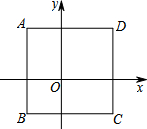 如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为(3,3).
如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为(3,3).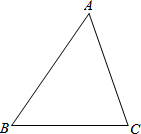 按要求在图中画图,并把答案填写在横线上.
按要求在图中画图,并把答案填写在横线上.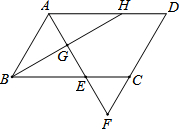 如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.
如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.