题目内容
如图1,梯形ABCD中,AD∥BC,AB=CD=AD=2cm,∠B=60°.
(1)可得梯形ABCD的周长L=______cm,面积S=______cm2;
(2)如图2,E、F分别为AD、BC边上的动点,连接EF.设BF=xcm,△BEF的面积为ycm2,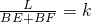 (k是常数).
(k是常数).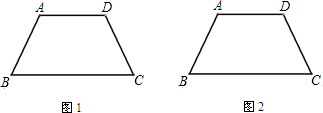
①试用含x的代数式表示y;
②如果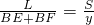 ,且k为整数,求BF的长.
,且k为整数,求BF的长.
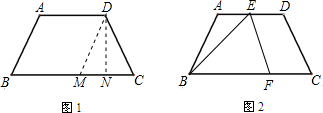 解:(1)如图1,作DM∥AB交BC与点M.则四边形ABMD是平行四边形,△DMC是等边三角形.
解:(1)如图1,作DM∥AB交BC与点M.则四边形ABMD是平行四边形,△DMC是等边三角形.则BM=AD=2cm,MC=DC=AB=2cm.
则梯形ABCD的周长=AD+AB+BC+CD=AB+AD+BM+MC+CD=10cm.
过点D作DN⊥BC,则DN=sin∠C•CD=sin60°•CD=
 ×2=
×2= ;
;故梯形ABCD的面积=(AD+BC)•DN÷2=3
 ;
;故答案是:10;3
 ;
;(2)如图2.
①∵△BEF与梯形ABCD等高,梯形ABCD的高DN=
 ,
,∴S△BEF=
 BF×
BF× =
=
 x,即y=
x,即y= x;
x;②∵
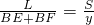 ,
,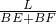 =k(k为常数),
=k(k为常数),∴ky=S,
∴k×
 x=3
x=3 ,
,∴x=
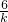 ,
,∵0<x≤4,k为整数,
∴x=1,2,3,
即BF的长为:1cm、2cm、3cm.
分析:(1)作DM∥AB交BC与点E.则四边形ABCD是平行四边形,△DMC是等边三角形,即可求得CD,BE的长度,从而求得该梯形的周长;过点D作DN⊥MC,在等边三角形DMC中利用特殊角的三角函数的定义求得DF的长度,根据梯形的面积公式解答即可;
(2)①根据三角形BEF的高与梯形ABCD的高相等,列出等式2y=
 x,从而用含x的代数表示y;
x,从而用含x的代数表示y;②根据
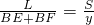 ,
,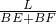 =k(k为常数),将已知量代入,即得到x(BF)的值.
=k(k为常数),将已知量代入,即得到x(BF)的值.点评:本题考查了平行四边形的判定,梯形周长,面积的计算,及函数思想.注意x的取值范围应该根据题中BC的长度来确定.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数. 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形? 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=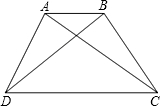 如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积.
如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积. 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=