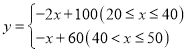题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,沿
上的动点,沿![]() 所在的直线折叠
所在的直线折叠![]() ,使点
,使点![]() 的对应点
的对应点![]() 始终落在边
始终落在边![]() 上,若
上,若![]() 为直角三角形,则
为直角三角形,则![]() 的长为_______.
的长为_______.
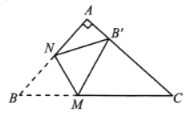
【答案】![]() 或
或![]()
【解析】
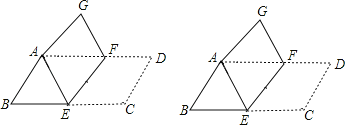
分两种情况讨论:如图1,当∠![]() =90°,此时
=90°,此时![]() 与A重合,M是BC的中点,进而可得结果;如图2,当∠
与A重合,M是BC的中点,进而可得结果;如图2,当∠![]() =90°,易得△
=90°,易得△![]() 是等腰直角三角形,从而可得CM=
是等腰直角三角形,从而可得CM=![]() ,再根据折叠的性质和已知条件即得关于BM的等式,进一步即可求出结果.
,再根据折叠的性质和已知条件即得关于BM的等式,进一步即可求出结果.
解:①如图1,当∠![]() =90°,此时
=90°,此时![]() 与A重合,M是BC的中点,
与A重合,M是BC的中点,
∴BM=![]() BC=
BC=![]() ;
;

②如图2,当∠![]() =90°,
=90°,
∵∠A=90°,AB=AC,
∴∠C=45°,
∴△![]() 是等腰直角三角形,
是等腰直角三角形,
∴CM=![]() ,
,

∵沿MN所在的直线折叠∠B,使点B的对应点为![]() ,
,
∴![]() ,
,
∴CM=![]() BM,
BM,
∵BC=![]() ,
,
∴CM+BM=![]() BM+BM=
BM+BM=![]() ,
,
∴BM=1,
综上所述,若△![]() 为直角三角形,则BM的长为
为直角三角形,则BM的长为![]() 或
或![]() ,
,
故答案为:1或![]() .
.

练习册系列答案
相关题目