题目内容
11.已知线段AB=10cm,C、D是AB上的两个黄金分割点,则线段CD的长为10$\sqrt{5}$-20cm.分析 根据黄金比值是$\frac{\sqrt{5}-1}{2}$,求出AD、BC的长,根据CD=AD+BC-AB代入计算得到答案.
解答 解: ∵C、D是AB上的两个黄金分割点,
∵C、D是AB上的两个黄金分割点,
∴AD=BC=$\frac{\sqrt{5}-1}{2}$AB=5$\sqrt{5}$-5,
∴CD=AD+BC-AB=10$\sqrt{5}$-20cm,
故答案为:10$\sqrt{5}$-20cm.
点评 此题主要是考查了黄金分割点的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值$\frac{\sqrt{5}-1}{2}$叫做黄金比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图,若a∥b,∠1=105°,则∠2的度数为( )
如图,若a∥b,∠1=105°,则∠2的度数为( )
 如图,若a∥b,∠1=105°,则∠2的度数为( )
如图,若a∥b,∠1=105°,则∠2的度数为( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
1.若|x-2|+(y+5)2=0,则yx=( )
| A. | 10 | B. | -10 | C. | 25 | D. | -25 |
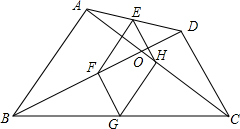 如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.
如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.