题目内容
1. 如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{3}$.
如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{3}$.(1)求证:四边形ABDE是平行四边形;
(2)求AB的长.
分析 (1)根据平行四边形的判定定理即可得到结论;
(2)由(1)知,AB=DE=CD,即D是CE的中点,在直角△CEF中利用三角函数即可求得到CE的长,则求得CD,进而根据AB=CD求解.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形;
(2)解:由(1)知,AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∴AB=CD=$\sqrt{3}$.
点评 本题考查了平行四边形的判定与性质,以及三角函数的应用,正确理解D是CE的中点是解题的关键.

练习册系列答案
相关题目
9.函数y=kx与y=-$\frac{k}{x}$在同一坐标系内的大致图象是( )
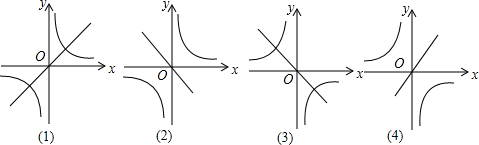

| A. | (1)和(2) | B. | (1)和(3) | C. | (2)和(3) | D. | (2)和(4) |
6.能用平方差公式进行计算的是( )
| A. | (2a-b)(-b+2a) | B. | (a-2b)(2a+b) | C. | (-2a-b)(2a+b) | D. | (-2a-b)(-2a+b) |
11.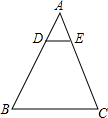 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}=\frac{1}{2}$,DE=4,则BC的长( )| A. | 8 | B. | 10 | C. | 12 | D. | 16 |