题目内容
下列方程没有实数根的个数是
(1) (2)
(2) (3)
(3) (4)x2-3x+5=0.
(4)x2-3x+5=0.
- A.1个
- B.2个
- C.3个
- D.4个
B
分析:(1)、(2)是无理方程,(3)是分式方程,(4)是一元二次方程,分别根据其解法,解答、判断即可.
解答:(1)由 得,
得,
∵ ≥0,
≥0,
∴ ≥1;
≥1;
∴方程没有实数根;
(2)由 得,
得,
两边平方、整理得,x2-x-3=0,
解得,x=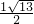 ,
,
经检验x=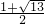 是增根,舍去;
是增根,舍去;
∴方程实数根是x=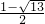 ;
;
(3)由 得,
得,
方程有意义则,x+1≠0,x≠-1,
解得,x=1,
∴方程有实数根;
(4)x2-3x+5=0,
∵△=9-20=-11<0,
∴方程没有实数根;
综上,方程没有实数根的个数是2.
故选B.
点评:本题考查了无理方程、分式方程及一元二次方程的解法,解无理方程的基本思想是把无理方程转化为有理方程来解,在变形时要注意根据方程的结构特征选择解题方法,用乘方法来解无理方程,往往会产生增根,应注意验根.
分析:(1)、(2)是无理方程,(3)是分式方程,(4)是一元二次方程,分别根据其解法,解答、判断即可.
解答:(1)由
 得,
得,∵
 ≥0,
≥0,∴
 ≥1;
≥1;∴方程没有实数根;
(2)由
 得,
得,两边平方、整理得,x2-x-3=0,
解得,x=
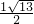 ,
,经检验x=
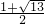 是增根,舍去;
是增根,舍去;∴方程实数根是x=
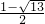 ;
;(3)由
 得,
得,方程有意义则,x+1≠0,x≠-1,
解得,x=1,
∴方程有实数根;
(4)x2-3x+5=0,
∵△=9-20=-11<0,
∴方程没有实数根;
综上,方程没有实数根的个数是2.
故选B.
点评:本题考查了无理方程、分式方程及一元二次方程的解法,解无理方程的基本思想是把无理方程转化为有理方程来解,在变形时要注意根据方程的结构特征选择解题方法,用乘方法来解无理方程,往往会产生增根,应注意验根.

练习册系列答案
相关题目
下列方程没有实数根的个数是( )
(1)
+1=0(2)
=-x(3)
=
(4)x2-3x+5=0.
(1)
| 3x+5 |
| x+3 |
| x |
| x+1 |
| 1 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列方程没有实数根的是( )
| A、x2-x-1=0 | ||
| B、x2-6x+5=0 | ||
C、x2-2
| ||
| D、2x2+x+1=0 |