题目内容
已知,M是等边△ABC边BC上的点 .
(1)(3分)如图1,过点M作MN∥AC,且交AB于点N ,求证:BM=BN;
(2)(7分)如图2,联结AM,过点![]() 作∠AMH=60°,MH与∠ACB的邻补角的平分线交与点H ,过H作HD
作∠AMH=60°,MH与∠ACB的邻补角的平分线交与点H ,过H作HD ![]() BC于点D.
BC于点D.
①求证: MA=MH; ②猜想写出CB,CM,CD之间的数量关系式,并加于证明;
(3)(4分)如图3,(2)中其它条件不变,若点M在BC延长线上时,(2)中两个结论还成立吗?若不成立请直接写出新的数量关系式(不必证明).



图1 图2 图3
(1)证明: ∵MN∥AC
∴∠BMN=∠C=60°,∠BNM=∠B=60°………1分
∴∠BMN=∠BNM………2分
∴BM=BN………3分
(2)①证明:过M点作MN∥AC交AB于N………4分
则BM=BN,∠ANM=120°
∵AB=AC ∴AN=MC
又因为CH是∠ACB外角平分线,所以∠ACH=60°
∴∠MCH=∠ACB+∠ACH=120°
又∵∠NMC=120°,∠AMH=60°
∴∠HMC+∠AMN=60°
 又∵∠NAM+∠AMN=∠BNM=60°
又∵∠NAM+∠AMN=∠BNM=60°
∴∠HMC=∠MAN
∴△AMN≌△MHC………6分
∴MA=MH………7分
②CB=CM+2CD………8分
证明:过M点作MG⊥AB于G
则△BMN为等边三角形,BM=2BG
在△BMG和△CHD中
∵HC=MN=BM, ∠B=∠HCD, ∠MGB=∠HDC
∴△BMG≌△CHD………9分
∴CD=BG ∴BM=2CD
所以BC=MC+2CD………10分
(3) (2)中结论①成立, ②不成立, ………12分
CB=2CD- CM ………14分

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案 明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
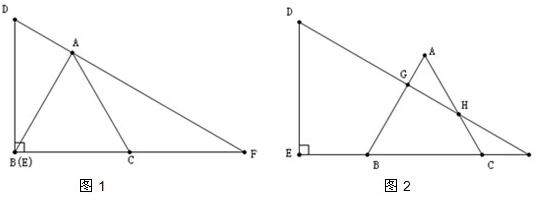
明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么? 19、已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线l上向右平移.当点E与点B重合时,点A恰好落在三角板的斜边DF上.
19、已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线l上向右平移.当点E与点B重合时,点A恰好落在三角板的斜边DF上.