题目内容
10. 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A(m,2).
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A(m,2).(1)求k的值;
(2)将直线y=2x向下平移交y轴于B,交双曲线于P,△AOP的面积为2,求直线PB的解析式.
分析 (1)把A(m,2)代入直线y=2x求出m=1,得出A(1,2),即可得出结果;
(2)作AM⊥x轴于M,PN⊥x轴于N,设P(a,b),则ab=2①,由梯形AMNP的面积得出$\frac{1}{2}$(2+b)(a-1)=2①,由①②求出a和b的值,得出P(1+$\sqrt{2}$,2$\sqrt{2}$-2),设直线PB的解析式为y=2x+b,把点P坐标代入求出b=-4即可.
解答 解:(1)把A(m,2)代入直线y=2x得:m=1,
∴A(1,2),
∴k=1×2=2;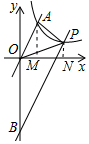
(2)作AM⊥x轴于M,PN⊥x轴于N,如图所示:
设P(a,b),则ab=2,
∵双曲线y=$\frac{2}{x}$,
∴△AOM的面积=△PON的面积=$\frac{1}{2}$×2=1,
∵△AOP的面积为2,
∴梯形AMNP的面积=2,即$\frac{1}{2}$(2+b)(a-1)=2①,
由①②得:$\left\{\begin{array}{l}{a=1+\sqrt{2}}\\{b=2\sqrt{2}-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=1-\sqrt{2}}\\{b=-2\sqrt{2}-2}\end{array}\right.$(舍去),
∴P(1+$\sqrt{2}$,2$\sqrt{2}$-2),
∵直线PB与直线y=2x平行,
∴设直线PB的解析式为y=2x+b,
把点P坐标代入得:2+2$\sqrt{2}$+b=2$\sqrt{2}$-2,
解得:b=-4,
∴直线PB的解析式为y=2x-4.
点评 此题主要考查了反比例函数与一次函数的交点,两条直线的平行关系、坐标与图形性质;求出点P的坐标是解决问题(2)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列各式中正确的是( )
| A. | -$\sqrt{49}$=-7 | B. | $\sqrt{49}$=±7 | C. | -$\sqrt{49}$=±7 | D. | ±$\sqrt{49}$=7 |
15.化简(-5)2003+52004所得的值为( )
| A. | -5 | B. | 0 | C. | 52002 | D. | 4×52003 |
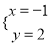 是二元一次方程组
是二元一次方程组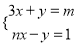 的
的 解,则m-n的值是( )
解,则m-n的值是( )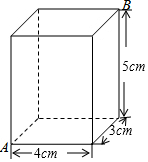 图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?
图是一个长、宽、高分别为4cm,3cm,5cm的长方体,一只蚂蚁从顶点A出发,沿长方体的表面爬行至点B,爬行的最短路程是多少?