题目内容
19.观察下面的变形规律:$\frac{1}{1×2}$=1-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$;…解答下面的问题:
(1)若n为正整数,请你猜想:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)求和:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2010×2011}$=$\frac{2010}{2011}$.
分析 (1)根据变形规律直接可以写出答案.
(2)根据规律展开即可化简求值.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故答案为$\frac{1}{n}$-$\frac{1}{n+1}$
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2010}$-$\frac{1}{2011}$=1-$\frac{1}{2011}$=$\frac{2010}{2011}$.
故答案为$\frac{2010}{2011}$.
点评 本题考查分数的加法法则,运用规律把分数拆为两个分数的差是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.-2的倒数的绝对值( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
9.-$\frac{1}{2}$是$\frac{1}{2}$的( )
| A. | 倒数 | B. | 绝对值 | C. | 相反数 | D. | 平方 |
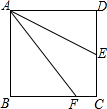 如图,在四边形ABCD中,∠C=∠D=90°,E是CD中点,F是BC上一点,且AE平分∠DAF,求证:AF=AD+CF.
如图,在四边形ABCD中,∠C=∠D=90°,E是CD中点,F是BC上一点,且AE平分∠DAF,求证:AF=AD+CF.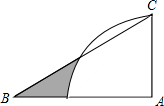 如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为9$\sqrt{3}$-3π.(结果保留π)
如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为9$\sqrt{3}$-3π.(结果保留π)
 小刚同学在一个正方体盒子的每个面都写了一个字,分别是:我、喜、欢、数、学、课.其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )
小刚同学在一个正方体盒子的每个面都写了一个字,分别是:我、喜、欢、数、学、课.其平面展开图如图所示,那么在该正方体盒子中,和“我”相对的面所写的字是( )