Question

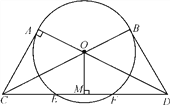
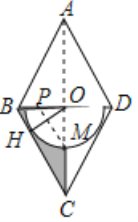
【题目】如图，在菱形ABCD中，连结BD、AC交于点O，过点O作于点H，以点O为圆心，OH为半径的半圆交AC于点M．

①求证：DC是⊙O的切线．

②若且，求图中阴影部分的面积．

③在②的条件下，P是线段BD上的一动点，当PD为何值时，的值最小，并求出最小值．

Answer 1

【答案】①证明见解析；②③

【解析】

①作，证明OH为圆的半径，即可求解；

②利用，即可求解；

③作M关于BD的对称点N，连接HN交BD于点P，，此时最小，即可求解．

解：①过点O作，垂足为G，

在菱形ABCD中，AC是对角线，则AC平分∠BCD，

∵，，

∴，

∴OH、OG都为圆的半径，即DC是⊙O的切线；

②∵且，

∴，

，

∴，

在直角三角形OHC中，，

∴，，

∴，

；

③作M关于BD的对称点N，连接HN交BD于点P，

∵，

∴，此时最小，

∵，

，

∴，

∴，

∴，

即：PH+PM的最小值为，

在Rt△NPO中，

，

在Rt△COD中，

，

则．