题目内容
6.(1)解方程:$\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3(2)计算:(2m-1n-2)-2•(-$\frac{3m}{4{n}^{3}}$)÷(-$\frac{{m}^{2}n}{2}$)
分析 (1)先把分式方程化为整式方程,再求出x的值,代入公分母进行检验即可;
(2)从左到右依次计算即可.
解答 解:(1)去分母得,1=-(1-x)-3(x-2),
去括号得,1=-1+x-3x+6,
移项,合并同类项得,2x=4,
系数化为1得,x=2,
检验:当x=2时,x-2=0,
故原方程无解;
(2)原式=$\frac{1}{4}$m2n4•(-$\frac{3m}{4{n}^{3}}$)•(-$\frac{2}{{m}^{2}n}$)
=-$\frac{3{m}^{3}n}{16}$•(-$\frac{2}{{m}^{2}n}$)
=$\frac{3m}{8}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
1. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 肇 | D. | 庆 |
15.下列计算正确的是( )
| A. | 6a3•6a4=6a7 | B. | (2+a)2=4+2a+a2 | C. | (3a3)2=6a6 | D. | (π-3.14)0=1 |
 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,OF⊥CD.
如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,OF⊥CD.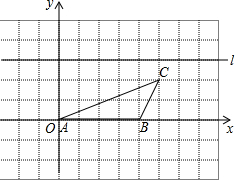 如图,在平面直角坐标系中,△ABC的边AB与x轴重合,点C的坐标是(5,2),在△ABC的上方有一直线l与x轴平行;
如图,在平面直角坐标系中,△ABC的边AB与x轴重合,点C的坐标是(5,2),在△ABC的上方有一直线l与x轴平行;