题目内容
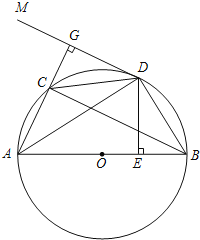
【题目】如图，AB是
的直径，D是
的中点，
于E，交CB于点
过点D作BC的平行线DM，连接AC并延长与DM相交于点G．
求证：GD是的切线；
求证：
；
若
，
，求
的值．
【答案】（1）证明见解析（2）证明见解析（3）
【解析】
连接OD，由垂径定理得出
，OD平分BC，由圆周角定理得出
，证出
，即可得出GD是
的切线；
由切割线定理即可得出结论；
由垂径定理得出
，
，由勾股定理求出
，证明
∽
，得出对应边成比例
，由圆周角定理得出
，求出BH，得出DH、AH、CH，求出BC的长，再由三角函数的定义即可得出结果．
证明：连接OD，如图所示：
是
的中点，
，OD平分BC，
是的直径，
，即
，
，
，
是的切线；
证明：
是的切线，AG是的割线，
；
解：是的中点，
，
，
，
，
，
∽，
，
是的直径，
，
，
，
，
，
，
，
，
．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
