题目内容
如图，在△ABC中，EF∥BC，| AE |
| EB |
| 1 |
| 2 |
考点：相似三角形的判定与性质
专题：
分析：由EF∥BC，可知△AEF∽△ABC，由相似三角形的性质可知
=（
）2=（
）2=
，设S△ABC=x，则S△AEF=x-8，列出比例式求解即可．
| S△AEF |
| S△ABC |
| AE |
| AB |
| 1 |
| 3 |
| 1 |
| 9 |
解答：解：∵
=
，∴
=
．
∵EF∥BC，∴△AEF∽△ABC，
∴
=（
）2=（
）2=
，
设S△ABC=x，则S△AEF=x-8，
∴
=
，
解得x=9．
故答案为：9．
| AE |
| EB |
| 1 |
| 2 |
| AE |
| AB |
| 1 |
| 3 |
∵EF∥BC，∴△AEF∽△ABC，
∴
| S△AEF |
| S△ABC |
| AE |
| AB |
| 1 |
| 3 |
| 1 |
| 9 |
设S△ABC=x，则S△AEF=x-8，
∴
| x-8 |
| x |
| 1 |
| 9 |
解得x=9．
故答案为：9．
点评：本题考查了相似三角形的判定与性质．关键是由平行得三角形相似，利用相似三角形的性质求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，在等边三角形ABC中，∠ABC，∠ACB的平分线交于点F，过点F作DE∥BC，分别与AB、AC交于点D、E．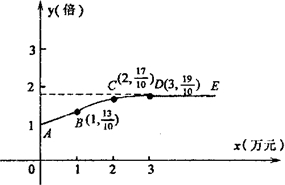
某公司生产一种产品，每件成本3元，售价4元，年销售量20万件，为获得更好的效益，公司准备拿出一定资金做广告．根据经验，设广告费x万元，做广告后的年销售量是原销售量的y倍，且y与x的关系