题目内容
| |||||||||||||||||||
答案:
解析:
提示:
解析:
(1) |
解:因为BD⊥AE于D点,CE⊥AE于E点(已知) 所以∠ADB=∠AEC= 因为∠BAC= 所以∠ABD+∠BAD=∠CAE+∠BAD= 所以∠ABD=∠CAE(同角的余角相等) 在△ABD和△CAE中, 所以△ABD≌△CAE(AAS) 所以BD=AE,AD=CE(全等三角形的对应边相等) 又因为AE=AD+DE,所以BD=CE+DE |
(2) |
BD=DE-CE.证法与(1)相同. |
(3) |
BD=DE-CE. |
(4) |
归纳前三个小题结论表述如下:当B、C在AE异侧时,BD=DE+CE;当B、C在AE同侧时,BD=DE-CE. |
提示:
|
提示:解这类题的关键是猜想规律,再运用几何知识予以说明. |

练习册系列答案
相关题目
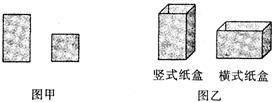 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖的长方体纸盒.(长方形的宽与正方形的边长相等)
某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种无盖的长方体纸盒.(长方形的宽与正方形的边长相等)(1)现有正方形纸板50张,长方形纸板l 00张,若要做竖式纸盒x个,横式纸盒y个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | |
| 长方形纸板(张) | 3y |
(2)若有正方形纸板80张,长方形纸板n张,做成上述两种纸盒,纸板恰好全部用完.已知162<n<172,求n的值.





 S关于时间t的函数图象如图乙,若AB=6,则图乙中a、b的值正确的为( )
S关于时间t的函数图象如图乙,若AB=6,则图乙中a、b的值正确的为( )