题目内容
正方形ABCD和正方形A′B′C′D′边长均为(2+
)(3+
),中心O各边都互相重合.

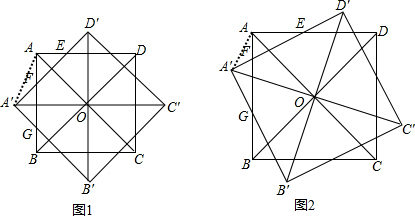
(1)正方形A′B′C′D′绕着中心O,逆时针方向旋转45°时(如图1),求证:△AEF≌△A′GF.
(2)正方形A′B′C′D′绕着中心O,逆时针方向旋转任意锐角时(如图2),
①指出△AEF的不变量;
②当锐角由30°到45°时求△AEF面积的取值范围.
| 2 |
| 3 |

(1)正方形A′B′C′D′绕着中心O,逆时针方向旋转45°时(如图1),求证:△AEF≌△A′GF.
(2)正方形A′B′C′D′绕着中心O,逆时针方向旋转任意锐角时(如图2),
①指出△AEF的不变量;
②当锐角由30°到45°时求△AEF面积的取值范围.
考点:全等三角形的判定与性质,正方形的性质,旋转的性质
专题:
分析:(1)连接OA=OA′,利用正方形的性质,得出出AF=A′F,证得△AEF≌△A′GF即可;
(2)①由(1)中的全等得出△AEF的周长不变等于正方形边长;
②分当旋转的锐角为30°时与旋转的锐角为45°时,求得各自的面积,得出答案即可.
(2)①由(1)中的全等得出△AEF的周长不变等于正方形边长;
②分当旋转的锐角为30°时与旋转的锐角为45°时,求得各自的面积,得出答案即可.
解答:(1)证明:如图,
连接AA′,则OA=OA′,
∴∠OAA′=∠OA′A,
∵∠FAO=FA′O=45°,
∴∠FAA′=∠FA′A,
∴AF=A′F,
在△AEF和△A′GF中,
∴△AEF≌△A′GF(ASA).
(2)①同理可证△AEF≌△A′GF,由此可得△AEF的周长不变等于正方形边长.
②当旋转的锐角为30°时,设AF=x,则EF=2x,AE=
x,
三边之和为(3+
)x=(2+
)(3+
),
因此x=(2+
).
s=3
+2
当旋转的锐角为45°时,设AF=y 则AE=y,EF=
y,
三边之和为(2+
)y=(2+
)(3+
),
因此y=(3+
).
s=6+3
.
由于旋转过程中△AEF的周长不变,而当旋转的锐角由30°到45°时△AEF的面积也逐步增大3
+2
≤s≤6+3
.

连接AA′,则OA=OA′,
∴∠OAA′=∠OA′A,
∵∠FAO=FA′O=45°,
∴∠FAA′=∠FA′A,
∴AF=A′F,
在△AEF和△A′GF中,
|
∴△AEF≌△A′GF(ASA).
(2)①同理可证△AEF≌△A′GF,由此可得△AEF的周长不变等于正方形边长.
②当旋转的锐角为30°时,设AF=x,则EF=2x,AE=
| 3 |
三边之和为(3+
| 3 |
| 2 |
| 3 |
因此x=(2+
| 2 |
s=3
| 3 |
| 6 |
当旋转的锐角为45°时,设AF=y 则AE=y,EF=
| 2 |
三边之和为(2+
| 2 |
| 2 |
| 3 |
因此y=(3+
| 3 |
s=6+3
| 3 |
由于旋转过程中△AEF的周长不变,而当旋转的锐角由30°到45°时△AEF的面积也逐步增大3
| 3 |
| 6 |
| 3 |
点评:此题考查三角形全等的判定与性质,正方形的性质,旋转的性质,以及含30°、45°直角三角形的性质的综合运用.

练习册系列答案
相关题目
在1,
,
,
,
,0.3131131113…中,无理数共有( )
| 22 |
| 7 |
| 3 |
| 3 | 27 |
| π |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
深圳是一个美丽的海滨城市,海岸线长约230000米,东临大亚湾,西濒珠江口,数据230000用科学记数法表示为( )
| A、23×104 |
| B、2.3×105 |
| C、2.3×106 |
| D、0.23×107 |
 如图,△ABC中,∠CAB+∠CBA=120°,点D,E分别在边AC,BC上,且AD=BE,以DE为边作等边△DEF,连接AF,BF.
如图,△ABC中,∠CAB+∠CBA=120°,点D,E分别在边AC,BC上,且AD=BE,以DE为边作等边△DEF,连接AF,BF. 如图,等边△ABC内接于⊙O,P是
如图,等边△ABC内接于⊙O,P是
 如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,
如图,∠AOC=∠BOD=90°,OE是∠AOB的平分线,且∠COE=75°,