题目内容
 如图,△ABC等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置.
如图,△ABC等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置.(1)旋转中心是点
A
A
;(2)旋转角最少是
60
60
度;(3)如果点M是AB上的一点,那么经过上述旋转后,点M旋转到什么位置?请在图中将点M的对应点M′表示出来;
(4)如果AM=2,请计算点M旋转到M′过程中所走过的最短的路线长度(结果保留π);
(5)如果等边三角形△ABC的边长为6,求四边形ADCE的面积.
分析:(1)根据旋转的性质,对应边的交点即为旋转中心;
(2)根据旋转的性质,对应边的夹角为旋转角;
(3)根据旋转的性质,点M′在AB的对应边AC上;
(4)利用弧长公式列式进行计算即可得解;
(5)根据旋转变换不改变图形的大小可得△ABD和△ACE全等,从而得到四边形ADCE的面积=△ABC的面积,然后列式进行计算即可得解.
(2)根据旋转的性质,对应边的夹角为旋转角;
(3)根据旋转的性质,点M′在AB的对应边AC上;
(4)利用弧长公式列式进行计算即可得解;
(5)根据旋转变换不改变图形的大小可得△ABD和△ACE全等,从而得到四边形ADCE的面积=△ABC的面积,然后列式进行计算即可得解.
解答: 解:(1)旋转中心为点A;
解:(1)旋转中心为点A;
(2)∵△ABC为等边三角形,
∴旋转角为∠BAC=60°;
故答案为:(1)A,(2)60;
(3)点M′在AC上,位置如图所示;
(4)最短的路线长度=
=
π;
(5)∵△ABD经过旋转后到达△ACE的位置,
∴△ABD≌△ACE,
∴S四边形ADCE=S△ADC+S△ACE=S△ADC+S△ABD=S△ABC,
∵等边△ABC的边长为6,
∴S△ABC=
×6×(
×6)=9
.
 解:(1)旋转中心为点A;
解:(1)旋转中心为点A;(2)∵△ABC为等边三角形,
∴旋转角为∠BAC=60°;
故答案为:(1)A,(2)60;
(3)点M′在AC上,位置如图所示;
(4)最短的路线长度=
| 60•π•2 |
| 180 |
| 2 |
| 3 |
(5)∵△ABD经过旋转后到达△ACE的位置,
∴△ABD≌△ACE,
∴S四边形ADCE=S△ADC+S△ACE=S△ADC+S△ABD=S△ABC,
∵等边△ABC的边长为6,
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评:本题考查了旋转的性质,等边三角形的性质以及弧长的计算,是基础题,熟记旋转的性质是解题的关键.

练习册系列答案
相关题目
 12、如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是
12、如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是 9、如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC中,从△BOF到△COD需要经过的变换是( )
9、如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC中,从△BOF到△COD需要经过的变换是( )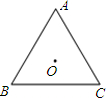 如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°.
如图,△ABC是边长为a的等边三角形,O为△ABC的中心.将△ABC绕着中心O旋转120°. 已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: 如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是( )
如图,在等边△ABC中,AC=3,点O在AC上,且AO=1.点P是AB上一点,连接OP,以线段OP为一边作正△OPD,且O、P、D三点依次呈逆时针方向,当点D恰好落在边BC上时,则AP的长是( )