题目内容
若实数xy满足4x2+y2-4x+6x+10=0,求x2+y2.
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:把4x2+y2-4x+6x+10=0化为4x2-4x+1+y2+6x+9=0,然后组成完全平方形式,从而出现2个非负数的和等于0的形式,那么每一个非负数都等于0,从而求出x、y的值即可,问题得以解决.
解答:解:∵4x2+y2-4x+6x+10=0,
∴4x2-4x+1+y2+6x+9=0,
∴(2x-1)2+(y+3)2=0,
∴2x-1=0,y+3=0,
∴x=
,y=-3,
∴x2+y2
=
+9
=9
.
∴4x2-4x+1+y2+6x+9=0,
∴(2x-1)2+(y+3)2=0,
∴2x-1=0,y+3=0,
∴x=
| 1 |
| 2 |
∴x2+y2
=
| 1 |
| 4 |
=9
| 1 |
| 4 |
点评:本题考查了配方法的应用、非负数的性质.记住完全平方公式:(a±b)2=a2±2ab+b2.

练习册系列答案
相关题目
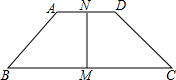 如图,AD∥BC,AB=CD,M是BC的中点,N是AD的中点,AD=5,BC=13,∠B+∠C=90°,求MN的长.
如图,AD∥BC,AB=CD,M是BC的中点,N是AD的中点,AD=5,BC=13,∠B+∠C=90°,求MN的长. 如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE.
如图,在△ABC中,∠A=100°,∠ABC=40°,BD是∠ABC的平分线,延长BD至E,使DE=AD.求证:BC=AB+CE. 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.