题目内容
15.若P(m,a),Q($\frac{1}{m}$,b)两点均在函数y=-$\frac{2}{x}$的图象上,且-1<m<0,则a-b的值为( )| A. | 正数 | B. | 负数 | C. | 零 | D. | 非负数 |
分析 根据反比例函数图象上点的坐标特征,把P和Q点坐标代入得a=-$\frac{2}{m}$,b=-$\frac{2}{\frac{1}{m}}$=-2m,则a-b=-2•$\frac{1-{m}^{2}}{m}$,然后利用m的范围确定a-b的符合即可.
解答 解:把P(m,a),Q($\frac{1}{m}$,b)代入y=-$\frac{2}{x}$得a=-$\frac{2}{m}$,b=-$\frac{2}{\frac{1}{m}}$=-2m,
所以a-b=-$\frac{2}{m}$+2m=-2•$\frac{1-{m}^{2}}{m}$,
因为-1<m<0,
所以1-m2>0,
所以a-b>0.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.已知点P1(x1,y1)、P2(x2,y2)在双曲线y=$\frac{3}{x}$上,下列说法中,正确的是( )
| A. | 若x1>x2,则y1>y2 | B. | 若x1>x2,则y1<y2 | ||
| C. | 若x1>x2>0,则y1>y2 | D. | 若x1>x2>0,则y1<y2 |
6.据报道,西部地区最大的客运枢纽系统--重庆西站,一期工程已经完成90%,预计在年内建成投入使用.届时,预计每年客流量可达42000000人次,将数42000000用科学记数法表示为4.2×107.
3.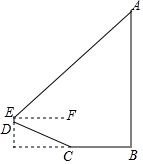 位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
 位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 AB进行了测量.如图,他们从塔底A的点B出发,沿水平方向行走了13米,到达点C,然后沿斜坡CD继续前进到达点D处,已知DC=BC.在点D处用测角仪测得塔顶A的仰角为42°(点A,B,C,D,E在同一平面内).其中测角仪及其支架DE高度约为0.5米,斜坡CD的坡度(或坡比)i=1:2.4,那么文峰塔的高度AB约为( )(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)| A. | 22.5 米 | B. | 24.0 米 | C. | 28.0 米 | D. | 33.3 米 |
10.要使式子$\frac{5x}{\sqrt{x+2}}$有意义,则x的取值范围是( )
| A. | x≠2 | B. | x>-2 | C. | x<-2 | D. | x≠-2 |
20.已知点P的坐标是(4,-6),则点P到x轴的距离是( )
| A. | 4 | B. | 6 | C. | -6 | D. | 4或6 |
4.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. | 正六边形 | B. | 正五边形 | C. | 平行四边形 | D. | 正三角形 |
5.点P(3,-1)关于坐标原点对称点为( )
| A. | (3,1) | B. | (-3,1) | C. | (-1,3) | D. | (-3,-1) |
