题目内容
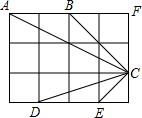 如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=
(2)判断△ABC与△DEC是否相似,并证明你的结论.
考点:相似三角形的判定,勾股定理
专题:
分析:(1)先在Rt△BCG中根据等腰直角三角形的性质求出∠GBC的度数,再根据∠ABC=∠GBC+∠ABG即可得出∠ABC的度数;在Rt△BCH中利用勾股定理即可求出BC的长.
(2)利用格点三角形的知识求出AB,BC及CE,DE的长度,继而可作出判断.
(2)利用格点三角形的知识求出AB,BC及CE,DE的长度,继而可作出判断.
解答: 解:(1)∵△BCG是等腰直角三角形,
解:(1)∵△BCG是等腰直角三角形,
∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴BC=
=
=2
.
故答案为:135°;2
;
(2)相似.理由如下:
∵BC=2
,EC=
,
∴
=
=
,
=
=
,
∴
=
,
又∵∠ABC=∠CED=135°,
∴△ABC∽△DEC.
 解:(1)∵△BCG是等腰直角三角形,
解:(1)∵△BCG是等腰直角三角形,∴∠GBC=45°,
∵∠ABG=90°,
∴∠ABC=∠GBC+∠ABG=90°+45°=135°;
∵在Rt△BHC中,BH=2,CH=2,
∴BC=
| BH2+CH2 |
| 22+22 |
| 2 |
故答案为:135°;2
| 2 |
(2)相似.理由如下:
∵BC=2
| 2 |
| 2 |
∴
| AB |
| CE |
| 2 | ||
|
| 2 |
| BC |
| DE |
2
| ||
| 2 |
| 2 |
∴
| AB |
| CE |
| BC |
| DE |
又∵∠ABC=∠CED=135°,
∴△ABC∽△DEC.
点评:此题主要考查学生对勾股定理和相似三角形的判定的理解和掌握,解答此题的关键是认真观察图形,得出两个三角形角和角,边和边的关系.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
抛物线y=x2-2x-1的对称轴是( )
| A、x=1 | B、x=-1 |
| C、x=2 | D、x=-2 |
若两圆的半径分别为4和3,圆心距为5,则这两圆的位置关系是( )
| A、内含 | B、相交 | C、内切 | D、外切 |
某电视机厂计划两年后产量为现在的2倍,如果每年增长率为x,则可得方程( )
| A、1+x2=3 |
| B、1+x=2 |
| C、1+2x=2 |
| D、(1+x)2=2 |
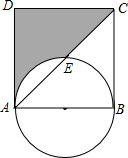 如图,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E.
如图,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E.