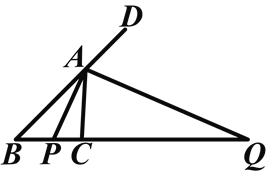题目内容
【题目】已知![]() 中,
中,![]() .
.
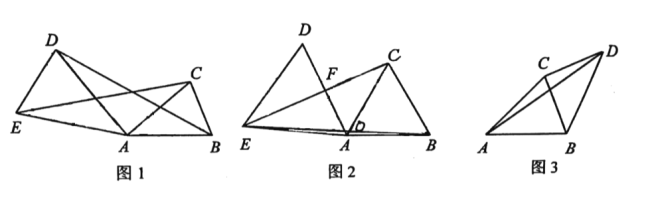
(1)如图1,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
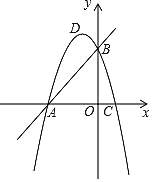
(2)如图2,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
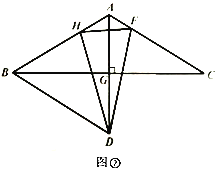
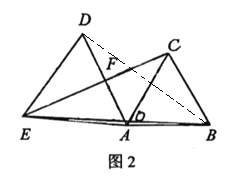
(3)如图3,在![]() 中,
中,![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证∠EAC=∠DAB.利用SAS证△ACE≌△ABD可得;(2)连接BD,证![]() ,证△ACE≌△ABD可得
,证△ACE≌△ABD可得![]() ,CE=BD=5,利用勾股定理求解;(3)作CE垂直于AC,且CE=AC,连接AE,则
,CE=BD=5,利用勾股定理求解;(3)作CE垂直于AC,且CE=AC,连接AE,则![]() ,利用勾股定理得AE
,利用勾股定理得AE![]() ,BE=
,BE=![]() ,根据(1)思路得AD=BE=
,根据(1)思路得AD=BE=![]() .
.
(1) 证明:∵∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
即∠EAC=∠DAB.
在△ACE与△ABD中,
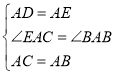 ,
,
∴△ACE≌△ABD(SAS),
∴![]() ;
;
(2)连接BD
因为![]() ,
, ![]() ,
,
所以![]() 是等边三角形
是等边三角形
因为![]() ,ED=AD=AE=4
,ED=AD=AE=4
因为![]()
所以![]()
同(1)可知△ACE≌△ABD(SAS),
所以![]() ,CE=BD=5
,CE=BD=5
所以![]()
所以BE=![]()
(3)作CE垂直于AC,且CE=AC,连接AE,则![]()
所以AE=![]()
因为![]()
所以AE![]()
又因为![]()
所以![]()
所以![]()
因为![]()
所以BC=CD, ![]()
因为同(1)可得△ACD≌△ECB(SAS)
所以AD=BE=![]()
所以![]()

练习册系列答案
相关题目