题目内容
已知一元二次方程x2-4x+3=0的两根是m,n且m<n.如图,若抛物线y=-x2+bx+c的图象经过点A(m,0)、B(0,n).
(1)求抛物线的解析式.
(2)若(1)中的抛物线与x轴的另一个交点为C.根据图象回答,当x取何值时,抛物线的图象在直线BC的上方?
(3)点P在线段OC上,作PE⊥x轴与抛物线交于点E,若直线BC将△CPE的面积分成相等的两部分,求点P的坐标.

解:(1)∵x2-4x+3=0的两个根为 x1=1,x2=3,
∴A点的坐标为(1,0),B点的坐标为(0,3),
又∵抛物线y=-x2+bx+c的图象经过点A(1,0)、B(0,3)两点,
∴ ,
,
∴抛物线的解析式为 y=-x2-2x+3,
答:抛物线的解析式是 y=-x2-2x+3.

(2)作直线BC,
由(1)得,y=-x2-2x+3,
∵抛物线y=-x2-2x+3与x轴的另一个交点为C,令-x2-2x+3=0,
解得:x1=1,x2=-3,
∴C点的坐标为(-3,0),
由图可知:当-3<x<0时,抛物线的图象在直线BC的上方,
答:当-3<x<0时,抛物线的图象在直线BC的上方.
(3)设直线BC交PE于F,P点坐标为(a,0),则E点坐标为(a,-a2-2a+3),
∵直线BC将△CPE的面积分成相等的两部分,
∴F是线段PE的中点(根据等底等高的三角形的面积相等),
即F点的坐标是(a, ),
),
∵直线BC过点B(0.3)和C(-3,0),
设直线BC的解析式是y=kx+b,代入得: ,
,
∴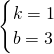
∴直线BC的解析式为y=x+3,
∵点F在直线BC上,
∴点F的坐标满足直线BC的解析式,
即 =a+3
=a+3
解得 a1=-1,a2=-3(此时P点与点C重合,舍去),
∴P点的坐标是(-1,0),
答:点P的坐标是(-1,0).
分析:(1)求出方程的解,得到B、A的坐标,代入抛物线得到方程组,求出方程组的解即可;
(2)求出C的坐标,根据B、C的坐标求出即可;
(3)设直线BC交PE于F,P点坐标为(a,0),则E点坐标为(a,-a2-2a+3),根据三角形的面积求出F的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出直线BC,把F的坐标代入求出即可.
点评:本题主要考查对用待定系数法求一次函数的解析式,二次函数与X轴的交点,解一元二次方程,解二元一次方程组,三角形的面积等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.
∴A点的坐标为(1,0),B点的坐标为(0,3),
又∵抛物线y=-x2+bx+c的图象经过点A(1,0)、B(0,3)两点,
∴
 ,
,∴抛物线的解析式为 y=-x2-2x+3,
答:抛物线的解析式是 y=-x2-2x+3.

(2)作直线BC,
由(1)得,y=-x2-2x+3,
∵抛物线y=-x2-2x+3与x轴的另一个交点为C,令-x2-2x+3=0,
解得:x1=1,x2=-3,
∴C点的坐标为(-3,0),
由图可知:当-3<x<0时,抛物线的图象在直线BC的上方,
答:当-3<x<0时,抛物线的图象在直线BC的上方.
(3)设直线BC交PE于F,P点坐标为(a,0),则E点坐标为(a,-a2-2a+3),
∵直线BC将△CPE的面积分成相等的两部分,
∴F是线段PE的中点(根据等底等高的三角形的面积相等),
即F点的坐标是(a,
 ),
),∵直线BC过点B(0.3)和C(-3,0),
设直线BC的解析式是y=kx+b,代入得:
 ,
,∴
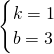
∴直线BC的解析式为y=x+3,
∵点F在直线BC上,
∴点F的坐标满足直线BC的解析式,
即
 =a+3
=a+3解得 a1=-1,a2=-3(此时P点与点C重合,舍去),
∴P点的坐标是(-1,0),
答:点P的坐标是(-1,0).
分析:(1)求出方程的解,得到B、A的坐标,代入抛物线得到方程组,求出方程组的解即可;
(2)求出C的坐标,根据B、C的坐标求出即可;
(3)设直线BC交PE于F,P点坐标为(a,0),则E点坐标为(a,-a2-2a+3),根据三角形的面积求出F的坐标,设直线BC的解析式是y=kx+b,把B、C的坐标代入求出直线BC,把F的坐标代入求出即可.
点评:本题主要考查对用待定系数法求一次函数的解析式,二次函数与X轴的交点,解一元二次方程,解二元一次方程组,三角形的面积等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目