题目内容
10.某航空公司规定旅客可随身携带一定质量的行李,若超过规定质量,则须购买行李票.已知行李票费用是行李质量的一次函数;行李质量60kg行李票费用6元,行李质量80kg行李票费用10元.旅客最多可免费携带行李的质量是( )| A. | 10kg | B. | 20kg | C. | 30kg | D. | 40kg |
分析 根据待定系数法列方程,求函数关系式,旅客可免费携带行李,即y=0,代入所求得的函数关系式,即可知质量为多少.
解答 解:设一次函数y=kx+b,由题意,得
$\left\{\begin{array}{l}{6=60k+b}\\{10=80k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=-6}\end{array}\right.$.
故一次函数的解析式为:y=$\frac{1}{5}$x-6(x≥30);
当y=0时,
$\frac{1}{5}$x-6=0,
x=30.
故旅客最多可免费携带30kg行李.
故选C.
点评 本题主要考查函数的图象和用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.注意自变量的取值范围不能遗漏.

练习册系列答案
相关题目
18.若P(P≥5)是一个质数而且P2-1除以24没有余数,则这种情况( )
| A. | 绝不可能 | B. | 只是有时可能 | C. | 总是可能 | D. | 只有当P=5时可能 |
19.下列运算正确的是( )
| A. | a3+a3=a6 | B. | a3•a4=a12 | C. | a6÷a3=a3 | D. | (a-b)2=a2-b2 |

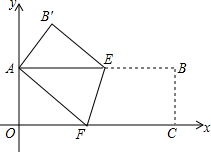 以点O为坐标原点,分别以矩形OABC的边OC,OA为x轴、y轴建立如图所示的直角坐标系,沿EF折叠矩形,使点C与点A重合,若顶点B的坐标为(9,3),则E点坐标为(5,4).
以点O为坐标原点,分别以矩形OABC的边OC,OA为x轴、y轴建立如图所示的直角坐标系,沿EF折叠矩形,使点C与点A重合,若顶点B的坐标为(9,3),则E点坐标为(5,4). 如图,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是多少?
如图,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是多少?