Question

【题目】请认真阅读下面的数学小探究，完成所提出的问题

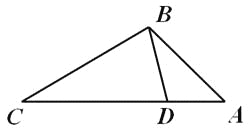
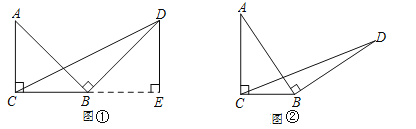
（1）探究1，如图①，在等腰直角三角形ABC中，∠ACB=90°，BC=3，将边 AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D作BC边上的高DE，则DE与BC的数量关系是 ． △BCD的面积为 ．

（2）探究2，如图②，在一般的Rt△ABC中，∠ACB=90°，BC=，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，请用含的式子表示△BCD的面积，并说明理由．

Answer 1

【答案】（1）DE=BC，4.5；（2）

【解析】

(1)证明△ACB≌△DEB，根据全等三角形的性质得到DE=AC=BC=3，根据三角形的面积公式计算；
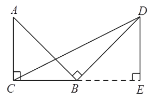
(2)作DG⊥CB交CB的延长线于G，证明△ACB≌△BGD，得到DG=BC=a，根据三角形的面积公式计算；

(1)∵△ABC是等腰直角三角形，

∴CA=CB，∠A=∠ABC=45°，
由旋转的性质可知，BA=BD，∠ABD=90°，
∴∠DBE=45°，
在△ACB和△DEB中，

，

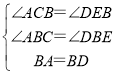∴△ACB≌△DEB(AAS)
∴DE=AC=BC=3，
∴；

故答案为：DE=BC，；

(2)作DG⊥CB交CB的延长线于G，

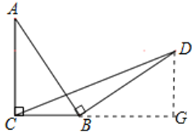
∵∠ABD=90°，
∴∠ABC+∠DBG=90°，又∠ABC+∠A=90°，
∴∠A=∠DBG，
在△ACB和△BGD中，

，

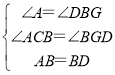∴△ACB≌△BGD(AAS)，
∴DG=BC=，

∴．