题目内容
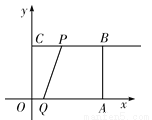
已知:如图所示,在平面直角坐标系xOy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动,设点P、点Q的运动时间为t(s).
(1)当t=1 s时,求经过点O,P,A三点的抛物线的解析式;
(2)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;
(3)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.
练习册系列答案
相关题目



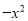 +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),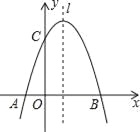
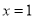 是关于
是关于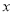 的方程
的方程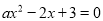 的一个根,则
的一个根,则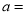 __________.
__________.