题目内容
11.解分式方程:(1)$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$;
(2)$\frac{x}{x+1}$=$\frac{2x}{3x+3}$+1.
分析 (1)方程两边同乘以(x+1)(x-1),化为整式方程进行解答即可;
(2)方程两边同乘以3(x+1),化为整式方程进行解答即可.
解答 解:(1)$\frac{2}{x-1}$=$\frac{4}{{x}^{2}-1}$
方程两边同乘以(x+1)(x-1),得
2(x+1)=4
解得,x=1.
检验,x=1时,(x+1)(x-1)=0.
故原分式方程无解.
(2)$\frac{x}{x+1}$=$\frac{2x}{3x+3}$+1.
方程两边同乘以3(x+1),得
3x=2x+3(x+1)
解得,x=-1.5.
检验:x=-1.5时,3(x+1)≠0.
故原分式方程的解是x=-1.5.
点评 本题考查解分式方程,解题的关键是将分式方程化为整式方程,注意最后要进行检验.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目




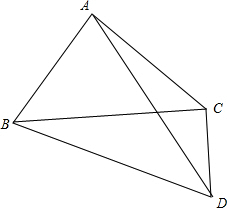 如图,在△ABC中,AB=AC,点D为△ABC外一点,连接AD,BD,CD,∠BAD=3∠CAD,∠ADC=30°,求证:∠DBC=30°.
如图,在△ABC中,AB=AC,点D为△ABC外一点,连接AD,BD,CD,∠BAD=3∠CAD,∠ADC=30°,求证:∠DBC=30°.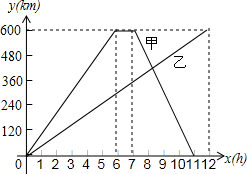 有甲、乙两辆汽车分别从相距600千米的A,B两地发出,相向而行,它们离开各自出发地的路程如图所示:
有甲、乙两辆汽车分别从相距600千米的A,B两地发出,相向而行,它们离开各自出发地的路程如图所示: 如图.已知:AB=6cm,BC=$\frac{1}{2}$AB,D为AC的中点,求DB的长.
如图.已知:AB=6cm,BC=$\frac{1}{2}$AB,D为AC的中点,求DB的长.